题目内容
9. 如图,直线AB、CD相交于点O,∠1-∠2等于50°,则∠2=115°,∠BOD=65°.
如图,直线AB、CD相交于点O,∠1-∠2等于50°,则∠2=115°,∠BOD=65°.
分析 根据邻补角的性质,可得∠1与∠2的关系,再根据∠1-∠2=50°,可得∠1与∠2,根据对顶角的性质,可得答案.
解答 解:由邻补角的性质,得∠1+∠2=180°,
∵∠1-∠2=50°,
则$\left\{\begin{array}{l}{∠1+∠2=180°}\\{∠1-∠2=50°}\end{array}\right.$,
解得$\left\{\begin{array}{l}{∠1=115°}\\{∠2=65°}\end{array}\right.$,
由对顶角相等,得∠BOD=∠1=65°.
故答案为:115°,65°.
点评 本题考查了对顶角、邻补角,解决本题的关键先由邻补角得出∠1与∠2的大小,再由对顶角得出答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.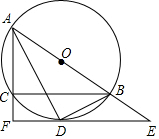 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
14.等边三角形ABC的边长AB=10cm,则这个三角形的BC边上的高为( )cm.
| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
1.下列命题是真命题的是( )
| A. | 同旁内角互补 | |
| B. | 三角形的一个外角等于它的两个内角之和 | |
| C. | 三角形的一个外角大于内角 | |
| D. | 直角三角形的两锐角互余 |
 如图,EA∥BD,∠BAC=∠BCA,∠ACD=110°,求∠EAB的度数.
如图,EA∥BD,∠BAC=∠BCA,∠ACD=110°,求∠EAB的度数. 如图AB与CD平行,∠1=45°,∠D=45°,
如图AB与CD平行,∠1=45°,∠D=45°, 尺规作图.
尺规作图.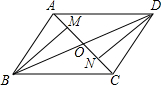 已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.
已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.