题目内容
19.计算(1)m•m3•(-m2)3
(2)(-0.25)2014×42015
(3)2(a2)3-a2•a4+(2a4)2÷a2
(4)($\frac{1}{3}$)-3-(3.14-π)0+(-2)4
(5)(p-q)4•(q-p)3•(p-q)2
(6)(-2x2)3+x2•x4-(-3x3)2.
分析 (1)根据幂的乘方、同底数幂的乘法即可解答本题;
(2)根据整式的乘法可以解答本题;
(3)根据幂的乘方和同底数幂的乘除法即可解答本题;
(4)根据负整数指数幂、零指数幂可以解答本题;
(5)根据同底数幂的乘法可以解答本题;
(6)根据积的乘方、同底数幂的乘法和合并同类项即可解答本题.
解答 解:(1)m•m3•(-m2)3
=m4•(-m6)
=-m10;
(2)(-0.25)2014×42015
=$(-\frac{1}{4})^{2014}×{4}^{2015}$
=4;
(3)2(a2)3-a2•a4+(2a4)2÷a2
=2a6-a6+4a8÷a2
=2a6-a6+4a6
=5a6;
(4)($\frac{1}{3}$)-3-(3.14-π)0+(-2)4
=27-1+16
=42;
(5)(p-q)4•(q-p)3•(p-q)2
=-(p-q)4•(p-q)3•(p-q)2
=(p-q)9;
(6)(-2x2)3+x2•x4-(-3x3)2
=(-8x6)+x6-9x6
=-16x6.
点评 本题考查整式的混合运算、零指数幂、负整数指数幂,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
7.2017年我市有5.6万名初中毕业生参加升学考试,为了解考生的数学成绩,从中抽取2000名考生的数学成绩进行统计,这个问题中样本是( )
| A. | 5.6万名考生 | B. | 2000名考生 | ||
| C. | 5.6万名考生的数学成绩 | D. | 2000名考生的数学成绩 |
14.等边三角形ABC的边长AB=10cm,则这个三角形的BC边上的高为( )cm.
| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
11.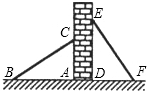 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )| A. | 60° | B. | 55° | C. | 65° | D. | 35° |
9.已知函数y=2x+b的图象过点(2,3),当 x=3时,y的值是( )
| A. | 4 | B. | 5 | C. | 8 | D. | 7 |