题目内容
14.先化简,再求值:$\frac{{{m^2}-2m+1}}{{{m^2}-1}}$÷(1+$\frac{m-1}{m+1}$)$-\frac{1}{2}$.其中m=tan60°.分析 先分解因式和计算括号内的加法,再算除法,最后算减法,再代入求出即可.
解答 解:$\frac{{{m^2}-2m+1}}{{{m^2}-1}}$÷(1+$\frac{m-1}{m+1}$)$-\frac{1}{2}$
=$\frac{(m-1)^{2}}{(m+1)(m-1)}$÷$\frac{2m}{m+1}$-$\frac{1}{2}$
=$\frac{m-1}{m+1}$•$\frac{m+1}{2m}$-$\frac{1}{2}$
=$\frac{m-1}{2m}$-$\frac{1}{2}$
=-$\frac{1}{2m}$,
当m=tan60°=$\sqrt{3}$时,原式=-$\frac{\sqrt{3}}{6}$.
点评 此题考查了分式的化简求值和特殊角的三角函数值的应用,熟练掌握运算法则是解本题的关键,注意运算顺序.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
4.下列运算错误的是( )
| A. | -(a-2b)=-a+2b | B. | a2•a3=a5 | C. | (a-2)2=a2+4 | D. | 3a-2a=a |
5.为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
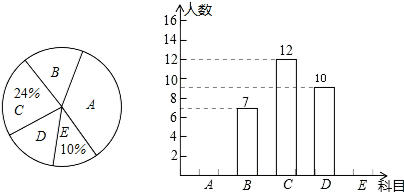

| A. | 选科目E的有5人 | |
| B. | 选科目D的扇形圆心角是72° | |
| C. | 选科目A的人数占体育社团人数的一半 | |
| D. | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6° |
3.在一个不透明的袋子中,装有红球、黄球、篮球、白球各1个,这些球除颜色外无其他差别,从袋中随机取出一个球,取出红球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
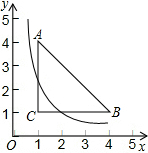 如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.
如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.