题目内容
19.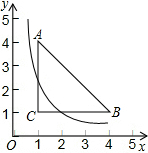 如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.
如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.
分析 结合图形可知当双曲线过C点时k有最小值,当直线AB与与双曲线只有一个交点时k有最大值,从而可求得k的取值范围.
解答 解:
若双曲线与△ABC有公共点,则双曲线向下最多到点C,向上最多到与直线AB只有一个交点,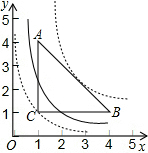
当过点C时,把C点坐标代入双曲线解析式可得1=$\frac{k}{1}$,解得k=1;
当双曲线与直线AB只有一个交点时,设直线AB解析式为y=ax+b,
∵A(1,4),B(4,1),
∴把A、B两点坐标代入可得$\left\{\begin{array}{l}{4=a+b}\\{1=4a+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$,
∴直线AB的解析式为y=-x+5,
联立直线AB和双曲线解析式可是$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=-x+5}\end{array}\right.$,消去y整理可得x2-5x+k=0,
则该方程有两个相等的实数根,
∴△=0,即(-5)2-4k=0,解得k=$\frac{25}{4}$,
∴k的取值范围为:1≤k≤$\frac{25}{4}$.
点评 本题主要考查一次函数和反比例函数的交点问题,确定出双曲线的两个端点位置是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
11.有4万个不小于70的两位数,从中随机抽取了3000个数据,统计如下:
请根据表格中的信息,估计这4万个数据的平均数约为( )
| 数据x | 70<x<79 | 80<x<89 | 90<x<99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78.1 | 85 | 91.9 |
| A. | 92.16 | B. | 85.23 | C. | 84.73 | D. | 77.97 |
8.今年我市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个.假设今年每个项目平均投资是x万元,那么下列方程符合题意的是( )
| A. | $\frac{106960}{x+500}$-$\frac{50760}{x}$=20 | B. | $\frac{50760}{x}$-$\frac{106960}{x+500}$=20 | ||
| C. | $\frac{106960}{x+20}$-$\frac{50760}{x}$=500 | D. | $\frac{50760}{x}$-$\frac{106960}{x+20}$=500 |

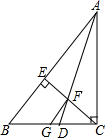 如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.
如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.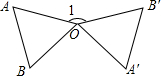 如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.
如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.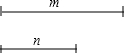 如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.
如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.