题目内容
6.有如图所示的直角边分别为1,2和2,2的直角三角形各2个.(1)请你利用这4个三角形,分别在8×8的网格纸上拼成2个周长不等的平行四边形;
(2)利用这样的4个三角形,你最多可以拼成多少个周长不等的平行四边形,其中最大的周长是多少(本小题只要求直接写出结果).

分析 (1)利用直角三角形的性质和平行四边形的性质结合网格得出答案;
(2)利用勾股定理以及平行四边形的性质得出即可.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:最多可以拼成4个周长不等的平行四边形,
最大的周长为:6+4$\sqrt{2}$.
点评 此题主要考查了应用设计与作图和平行四边形的性质以及勾股定理,根据题意熟练应用平行四边形的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.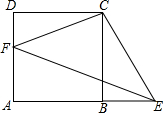 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
(1)求证:△CDF≌△CBE;
(2)如果正方形ABCD的面积为64,Rt△CEF的面积为50,则线段BE的长为多少?
 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°(1)求证:△CDF≌△CBE;
(2)如果正方形ABCD的面积为64,Rt△CEF的面积为50,则线段BE的长为多少?
15.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a3×a2=a6 | C. | (a3)3=a6 | D. | a8÷a2=a6 |
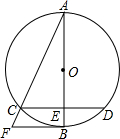 已知AB是⊙O的直径,CD是⊙O的弦,AB与CD交于E,CE=DE,过B作BF∥CD,交AC的延长线于点F,求证:BF是⊙O的切线.
已知AB是⊙O的直径,CD是⊙O的弦,AB与CD交于E,CE=DE,过B作BF∥CD,交AC的延长线于点F,求证:BF是⊙O的切线.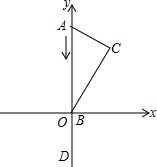 如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.
如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.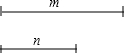 如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.
如图,已知线段m、n,利用直尺和圆规作图(不写作法,保留作图痕迹)作Rt△ABC,使∠ACB=90°,AB=m,BC=n.