题目内容
14.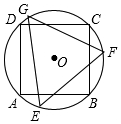 如图,正方形ABCD内接于⊙O,其边长为2,则⊙O的内接正三角形EFG的边长为$\sqrt{6}$.
如图,正方形ABCD内接于⊙O,其边长为2,则⊙O的内接正三角形EFG的边长为$\sqrt{6}$.
分析 连接AC、OE、OF,作OM⊥EF于M,先求出圆的半径,在Rt△OEM中利用30度角的性质即可解决问题.
解答 解;连接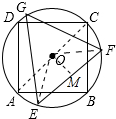 AC、OE、OF,作OM⊥EF于M,
AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=2,∠ABC=90°,
∴AC是直径,AC=2$\sqrt{2}$,
∴OE=OF=$\sqrt{2}$,
∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在Rt△OME中,∵OE=$\sqrt{2}$,∠OEM=$\frac{1}{2}$∠GEF=30°,
∴OM=$\frac{\sqrt{2}}{2}$,EM=$\sqrt{3}$OM=$\frac{\sqrt{6}}{2}$,
∴EF=$\sqrt{6}$.
故答案为$\sqrt{6}$.
点评 本题考查正多边形与圆、等腰直角三角形的性质、等边三角形的性质等知识,解题的关键是熟练应用这些知识解决问题,属于中考常考题型.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
4.宁城县打虎石水库,总库容量为11960万立方米,11960万用科学记数法表示为( )
| A. | 1.196×108 | B. | 1.196×107 | C. | 11.96×107 | D. | 0.1196×109 |
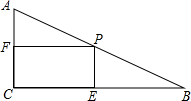 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.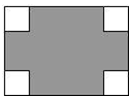 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.