题目内容
2．一个口袋中有3个大小相同的小球，球面上分别写有数字1、2、3，从袋中随机地摸出一个小球，记录下数字后放回，再随机地摸出一个小球．（1）求第一次摸出的球上的数字为奇数的概率；
（2）请用树状图或列表法求两次摸出的球上的数字和为奇数的概率．
分析 （1）直接利用概率公式求解；
（2）画树状图展示所有9种等可能的结果数，再找出两次摸出的球上的数字和为奇数的结果数，然后根据概率公式求解．
解答 解：（1）第一次摸出的球上的数字为奇数的概率=$\frac{2}{3}$；
（2）画树状图为：
共有9种等可能的结果数，其中两次摸出的球上的数字和为奇数的结果数为4，
所以两次摸出的球上的数字和为奇数的概率=$\frac{4}{9}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
练习册系列答案
同步练习强化拓展系列答案
相关题目
12．若对于任何实数a，b，c，d，定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，按照定义，若$|\begin{array}{l}{x+1}&{x}\\{x-1}&{2x-3}\end{array}|$=0，则x的值为（ ）
| A． | $\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | 3 | D． | ±$\sqrt{3}$ |
13．用火柴棒按下列方式搭建三角形：
（1）填表：
（2）当有n个三角形时，应用多少根火柴棒？（用含n的代数式表示）；
（3）当有2015根火柴棒时，照这样可以摆多少个三角形？
（1）填表：
| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
（3）当有2015根火柴棒时，照这样可以摆多少个三角形？
二次函数y=（x+m）2+n的图象如图，则反比例函数y=$\frac{mn}{x}$的图象经过第一、三象限．
7．下列式子中，能正确表示“x与y的倒数的和”是（ ）
| A． | $\frac{1}{x}$+$\frac{1}{y}$ | B． | $\frac{1}{x}$+y | C． | x+$\frac{1}{y}$ | D． | $\frac{1}{x+y}$ |
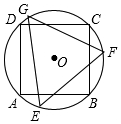如图，正方形ABCD内接于⊙O，其边长为2，则⊙O的内接正三角形EFG的边长为$\sqrt{6}$．
如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面与“生”相对应的面上的汉子是学．