题目内容
3.计算:(1)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
(2)$\frac{\sqrt{72}-\sqrt{32}}{\sqrt{8}}$-($\sqrt{3}$+2)2003($\sqrt{3}$-2)2004
(3)-22×6$\sqrt{0.5}$+3$\sqrt{2}$(3-2$\sqrt{2}$)-$\frac{1}{1+\sqrt{2}}$
(4)25(x+2)2-196=0.
分析 (1)先化简二次根式,再计算可得;
(2)先化简二次根式,再计算可得;
(3)先化简二次根式,再计算可得;
(4)直接开平方法求解可得.
解答 解:(1)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$÷2$\sqrt{3}$
=$\frac{14}{3}$;
(2)原式=$\frac{6\sqrt{2}-4\sqrt{2}}{2\sqrt{2}}$-[($\sqrt{3}$+2)($\sqrt{3}$-2)]2003•($\sqrt{3}$-2)
=1+$\sqrt{3}$-2
=-1+$\sqrt{3}$;
(3)原式=-4×3$\sqrt{2}$+9$\sqrt{2}$-12-$\sqrt{2}$+1
=-11-4$\sqrt{2}$;
(4)∵25(x+2)2=196,
∴(x+2)2=$\frac{196}{25}$,
则x+2=±$\frac{14}{5}$,
∴x=-2±$\frac{14}{5}$,
即x1=-$\frac{24}{5}$,x2=$\frac{4}{5}$.
点评 本题主要考查二次根式的化简和解方程的基本技能,熟练掌握二次根式的基本性质化简原式是解题的关键.

练习册系列答案
相关题目
13.用火柴棒按下列方式搭建三角形:

(1)填表:
(2)当有n个三角形时,应用多少根火柴棒?(用含n的代数式表示);
(3)当有2015根火柴棒时,照这样可以摆多少个三角形?

(1)填表:
| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
(3)当有2015根火柴棒时,照这样可以摆多少个三角形?
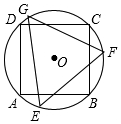 如图,正方形ABCD内接于⊙O,其边长为2,则⊙O的内接正三角形EFG的边长为$\sqrt{6}$.
如图,正方形ABCD内接于⊙O,其边长为2,则⊙O的内接正三角形EFG的边长为$\sqrt{6}$.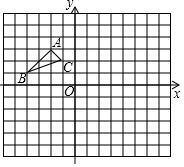 如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).
如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2). 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉子是学.
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉子是学.