题目内容
18．
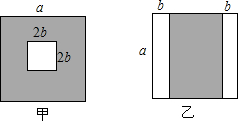如图，有甲、乙两种边长为a的正方形印花砖，阴影部分代表印花区域，空白部分代表留白区域，甲的留白区域是正方形，乙的留白区域是两个长方形．（1）甲的阴影部分的面积S甲=a2-4b2，乙的阴影部分的面积S乙=a2-2ab（用含a，b的代数式表示）
（2）当a=5b，求$\frac{{S}_{甲}}{{S}_{乙}}$的值．
分析 （1）利用正方形的面积差得出甲的面积，利用正方形的面积减去两个长方形的面积得出乙的面积；
（2）代入（1）中的代数式，求得甲乙面积，进一步代入得出答案即可．
解答 解：（1）甲的阴影部分的面积S甲=a2-4b2，乙的阴影部分的面积S乙=a2-2ab；
（2）当a=5b时，S甲=a2-4b2=21b2，乙的阴影部分的面积S乙=a2-2ab=15b2，
则$\frac{{S}_{甲}}{{S}_{乙}}$=$\frac{7}{5}$．
点评 此题考查列代数式，利用长方形和正方形的面积计算公式是解决问题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
9．用反证法证明：一个三角形中至少有一个内角小于或等于60°．在证明过程中，应先假设（ ）
| A． | 有一个内角大于60° | B． | 有一个内角小于60° | ||
| C． | 每一个内角都大于60° | D． | 每一个内角都小于60° |
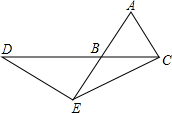等边三角形ABC的边长为1，点D在直线BC上，点E在直线AB上，且AE=2．若△ECD是以CD为底的等腰三角形，则CD的长为3．