��Ŀ����
5��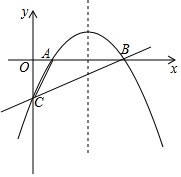 ��ͼ��������y=ax2+bx-2������A��1��0���͵�B��4��0������y�ύ�ڵ�C��
��ͼ��������y=ax2+bx-2������A��1��0���͵�B��4��0������y�ύ�ڵ�C����1���������ߵĽ���ʽ��
��2���Ե�AΪԲ�ģ�����ֱ��BC���еġ�A�����A�������
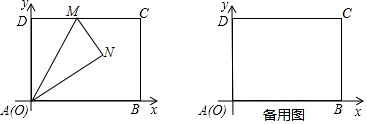
��3����ֱ��BC����ƽ��n����λ���������߽��ڵ�M��N�����߶�MN=2CB����ֱ��MN�Ľ���ʽ��ƽ�ƾ��룮
�����Ķ�����
������������•Τ�����緢��һԪ���η����и���ϵ���Ĺ�ϵΪ������֮�͵���һ����ϵ���������ϵ��֮�ȵ��෴��������֮�����ڳ������������ϵ��֮�ȣ����dz�֮ΪΤ�ﶨ����
������һԪ���η���ax2+bx+c=0������Ϊx1��x2����x1+x2=-$\frac{b}{a}$��x1•x2=$\frac{c}{a}$���������Τ�ﶨ������ʱ����ʹ�����Ϊ��
���� ��1���轻��ʽy=a��x-1����x-4������y=ax2-5ax+4a��Ȼ������4a=-2���a���ɵõ������߽���ʽ��
��2����AD��BC��D����ͼ����ȷ��C��0��-2���������BC=2$\sqrt{5}$����֤��Rt��BAD��Rt��BCO���������Ʊȿɼ����AD=$\frac{3\sqrt{5}}{5}$��Ȼ���������ߵ����ʵõ�Բ�İ뾶ΪAD��������Բ�������ʽ��⣻
��3�������ô���ϵ����ȷ��ֱ��BC�Ľ���ʽΪy=$\frac{1}{2}$x-2�������ֱ��MN�Ľ���ʽΪy=$\frac{1}{2}$x+t��M��x1��y1����N��x2��y2���������������Ľ�������õ�x1��x2Ϊ����-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=$\frac{1}{2}$x+2t�����������ø���ϵ���Ĺ�ϵ��x1+x2=4��x1•x2=2t+4����y1-y2=$\frac{1}{2}$��x1-x2�����������������ľ��빫ʽ����ȫƽ����ʽ�õ�MN=$\sqrt{\frac{5}{4}[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{-10t}$������$\sqrt{-10t}$=4$\sqrt{5}$���ⷽ�̵õ�t��ֵ���Ӷ��õ�ֱ��MN�Ľ���ʽ��Ȼ������ֱ��ƽ�ƵĹ���ȷ��ƽ�Ƶľ��룮
��� �⣺��1���������߽���ʽΪy=a��x-1����x-4����
��y=ax2-5ax+4a��
��4a=-2�����a=-$\frac{1}{2}$��
�������߽���ʽΪy=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2��
��2����AD��BC��D����ͼ�� ��x=0ʱ��y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=-2����C��0��-2����
��x=0ʱ��y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=-2����C��0��-2����
BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
�ߡ�ABD=��CBO��
��Rt��BAD��Rt��BCO��
��$\frac{AD}{OC}$=$\frac{AB}{BC}$����$\frac{AD}{2}$=$\frac{2}{2\sqrt{5}}$��
��AD=$\frac{3\sqrt{5}}{5}$��
��ֱ��BC���еġ�A��
��ADΪ��A�İ뾶��
���A�����=��•��$\frac{3\sqrt{5}}{5}$��2=$\frac{9}{5}$�У�
��3����ֱ��BC�Ľ���ʽΪy=kx+m��
��B��4��0����C��0��-2�������$\left\{\begin{array}{l}{4k+m=0}\\{m=-2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{m=-2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=$\frac{1}{2}$x-2��
��ֱ��MN�Ľ���ʽΪy=$\frac{1}{2}$x+t��M��x1��y1����N��x2��y2����
��x1��x2����-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=$\frac{1}{2}$x+2t��������
��������Ϊx2-4x+2t+4=0��
��x1+x2=4��x1•x2=2t+4��
��y1-y2=$\frac{1}{2}$x1+t-��$\frac{1}{2}$x2+t��=$\frac{1}{2}$��x1-x2����
��MN=$\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}$=$\sqrt{\frac{5}{4}��{x}_{1}-{x}_{2}��^{2}}$=$\sqrt{\frac{5}{4}[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{5}{4}[16-4��2t+4��]}$=$\sqrt{-10t}$��
��MN=2CB��
��$\sqrt{-10t}$=4$\sqrt{5}$�����t=-8��
��ֱ��MN�Ľ���ʽΪy=$\frac{1}{2}$x-8��
�ཫֱ��BC����ƽ��6����λ�õ�ֱ��MN����ƽ�Ƶľ���Ϊ6��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������ߵ����ʣ������ô���ϵ������һ�κ����Ͷ��κ�������ʽ����ͨ���ⷽ�������������Ľ������ꣻ�����������ľ��빫ʽ�����Ʊȼ����߶εij������Ӧ�ø���ϵ���Ĺ�ϵ��

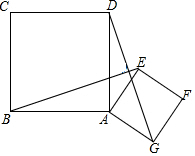 ��ͼ����֪������ABCD��������AEFG������BE��DG��
��ͼ����֪������ABCD��������AEFG������BE��DG��