题目内容
15．若直角三角形两条直角边的边长分别为15cm和12cm，那么此直角三角形斜边上的中线是$\frac{3\sqrt{41}}{2}$cm．分析 先根据勾股定理求出斜边的长，再由直角三角形的性质即可得出结论．
解答 解：∵在直角三角形中，两直角边为15cm，12cm，
∴斜边长=$\sqrt{1{5}^{2}+1{2}^{2}}$cm=3$\sqrt{41}$cm，
∵直角三角形中斜边的中线长为斜边长的一半，
∴斜边中线长为$\frac{3\sqrt{41}}{2}$cm，
故答案为：$\frac{3\sqrt{41}}{2}$．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图，已知△ABC中，∠ACB=90°，且AC=BC．过点C作一条射线CE⊥AE于点E，再过点B作BD⊥CE于点D．试证明AE=BD+DE．
如图：在△ABC中，CE、CF分别平分∠ACB与它的邻补角∠ACD，AE⊥CE于E，AF⊥CF于F，直线EF分别交AB、AC于M、N．
已知：如图，AD⊥BC于D，EG⊥BC于G，∠E=∠AFE．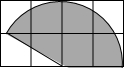
如图所示的格点纸中每个小正方形的边长均为1，以小正方形的顶点为圆心，2为半径做了一个扇形，用该扇形围成一个圆锥的侧面，针对此做法，小明和小亮通过计算得出以下结论：小明说此圆锥的侧面积为$\frac{5}{3}$π；小亮说此圆锥的弧长为$\frac{5}{3}$π，则下列结论正确的是（ ）
如图，抛物线y=ax2+bx-2经过点A（1，0）和点B（4，0），与y轴交于点C．