题目内容
16．木匠做一个矩形木框，长为80cm，宽为60cm，对角线的长为100cm，则这个木框合格（填“合格”或“不合格”）分析 只要算出桌面的长与宽的平方和是否等于对角线的平方，如果相等可得长、宽、对角线构成的是直角三角形，由此可得到每个角都是直角，根据矩形的判定：有三个角是直角的四边形是矩形，可得此桌面合格．
解答 解：解：∵802+602=10000=1002，
即：AD2+DC2=AC2，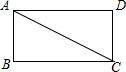
∴∠D=90°，
同理：∠B=∠BCD=90°，
∴四边形ABCD是矩形，
故答案为合格．
点评 本题考查的是勾股定理逆定理在实际中的应用，以及矩形的判定，关键是熟练掌握勾股定理逆定理与矩形的判定方法；勾股定理逆定理：在一个三角形中，两条边的平方和等于另一条边的平方，那么这个三角形就是直角三角形；矩形的判定方法：①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形．
练习册系列答案
相关题目
7．
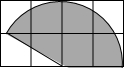如图所示的格点纸中每个小正方形的边长均为1，以小正方形的顶点为圆心，2为半径做了一个扇形，用该扇形围成一个圆锥的侧面，针对此做法，小明和小亮通过计算得出以下结论：小明说此圆锥的侧面积为$\frac{5}{3}$π；小亮说此圆锥的弧长为$\frac{5}{3}$π，则下列结论正确的是（ ）
如图所示的格点纸中每个小正方形的边长均为1，以小正方形的顶点为圆心，2为半径做了一个扇形，用该扇形围成一个圆锥的侧面，针对此做法，小明和小亮通过计算得出以下结论：小明说此圆锥的侧面积为$\frac{5}{3}$π；小亮说此圆锥的弧长为$\frac{5}{3}$π，则下列结论正确的是（ ）| A． | 只有小明对 | B． | 只有小亮对 | C． | 两人都对 | D． | 两人都不对 |
11．
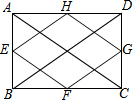如图，已知矩形ABCD的对角线AC，BD的长是6cm，E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH的周长是（ ）
如图，已知矩形ABCD的对角线AC，BD的长是6cm，E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH的周长是（ ）| A． | 18cm | B． | 16cm | C． | 15cm | D． | 12cm |
1．$\sqrt{\frac{16}{81}}$的算术平方根的倒数是（ ）
| A． | ±$\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{9}{4}$ | D． | $\frac{4}{9}$ |
如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=4，BC=6，将四个直角三角形中边长为4的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（ ）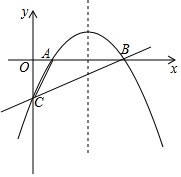
如图，抛物线y=ax2+bx-2经过点A（1，0）和点B（4，0），与y轴交于点C．