题目内容
12. 在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
分析 首先过点Q作QH∥OP,交OR的延长线于点H,证得△POR∽△QHR和△HOQ是等边三角形,进一步利用三角形的边关系整理得出答案即可.
解答 解:如图,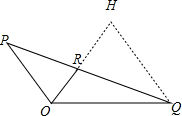
过点Q作QH∥OP,交OR的延长线于点H,
∵QH∥OP,
∴△POR∽△QHR,∠POR=∠H,
∴$\frac{HQ}{PO}$=$\frac{HR}{OR}$,
∵∠POQ=120°,∠POQ的平分线OR交PQ于点R,
∴∠POR=∠H=60°,
∴△HOQ是等边三角形,
∴OH=HQ=OQ,
∴$\frac{HQ}{PO}$=$\frac{HR}{OR}$=$\frac{OH-OR}{OR}$=$\frac{OH}{OR}$-1,
∴$\frac{HQ}{PO}$+1=$\frac{OH}{OR}$,
两边同除以OQ得$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
点评 此题考查三角形相似的判定与性质,等边三角形的判定与性质,掌握三角形相似的判定方法,正确作出辅助线是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是( )
| A. | x=3 | B. | x=-3 | C. | x=$\frac{3}{2}$ | D. | x=-$\frac{3}{2}$ |
1.在△ABC中,BC=15cm,CA=45cm,AB=57cm,另一个和它相似的三角形的最短边长是5cm,则最长边长是
( )
( )
| A. | 18cm | B. | 19cm | C. | 24cm | D. | 19.5cm |
2.已知点P到∠AOB两边的距离相等,若∠POB=45°,则∠AOB等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,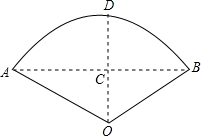 如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?
如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?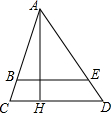 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.