题目内容
5.如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是( )| A. | x=3 | B. | x=-3 | C. | x=$\frac{3}{2}$ | D. | x=-$\frac{3}{2}$ |
分析 根据图象上函数值相等的点关于对称轴对称,可得抛物线的对称轴.
解答 解:由点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,得
(-2,-3)、(5,-3)关于对称轴对称,
即对称轴过(-2,-3)、(5,-3)的中点,
x=$\frac{-2+5}{2}$=$\frac{3}{2}$,
故选C.
点评 本题考查了二次函数的性质,图象上函数值相等点的垂直平分线是抛物线的对称轴.

练习册系列答案
相关题目
 如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.
如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.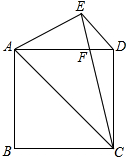 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AE=AF.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AE=AF. 在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.