题目内容
3.已知:∠AOB=60°,射线OC绕点O旋转,OD、OE分别是∠BOC和∠COA的平分线,求∠DOE的度数.分析 分类讨论:当OC在∠AOB内部,如图1,根据角平分线定义易得∠DOC=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,则∠DOE=∠DOC+∠COE=$\frac{1}{2}$∠AOB=30°;当OC在∠AOB外部,且靠近OB,如图2,根据角平分线定义得到∠DOC=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,则∠DOE=∠COE-∠COD=$\frac{1}{2}$∠AOB=30°;当OC在∠AOB外部,且靠近OA,如图3,同样可得到∠DOE=30°.
解答 解:当OC在∠AOB内部,如图1,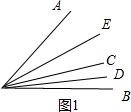
∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠DOC=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠DOC+∠COE=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°;
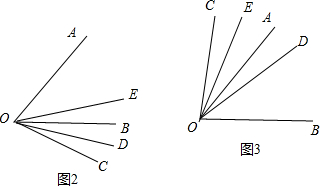
当OC在∠AOB外部,且靠近OB,如图2,
∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠DOC=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COE-∠COD=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°;
当OC在∠AOB外部,且靠近OA,如图3,同样可得到∠DOE=30°,
综上所述,∠DOE的度数为30°.
点评 本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.性质:若OC是∠AOB的平分线则∠AOC=∠BOC=$\frac{1}{2}$∠AOB或∠AOB=2∠AOC=2∠BOC.

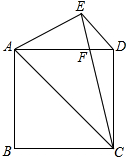 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AE=AF.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AE=AF.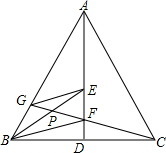 如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:
如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证: 在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$. 将含30°角的直角三角板的短直角边和含45°角的直角三角板的一条直角边如图放置,则∠1的度数为75度.
将含30°角的直角三角板的短直角边和含45°角的直角三角板的一条直角边如图放置,则∠1的度数为75度.