题目内容
7.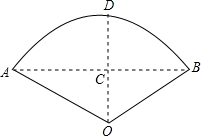 如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?
如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?
分析 由垂径定理可知AC=6$\sqrt{3}$,在Rt△ACO中利用勾股定理可求得AO=12,由特殊锐角三角函数可知∠AOC=60°,∠AOB=120°,所以管道的长度为$\frac{1}{3}$圆周长.
解答 解:∵OC⊥AB,AB=12$\sqrt{3}$,
∴AC=6$\sqrt{3}$.
设圆O的半径为r,则OA=r,OC=r-6.
在Rt△ACO中,由勾股定理得:AO2=OC2+AC2,即${r}^{2}=(r-6)^{2}+(6\sqrt{3})^{2}$.
解得:AO=12.
∴$\frac{AC}{AO}=\frac{6\sqrt{3}}{12}$=$\frac{\sqrt{3}}{2}$.
∴∠AOC=60°.
∴∠AOB=120°.
∴直管的长度=$\frac{1}{3}×2π×r$=$\frac{1}{3}×2×π×12$=8πm.
点评 本题主要考查的是垂径定理、勾股定理、特殊锐角三角函数值,求得圆O的半径和∠AOB的度数是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17. 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.