题目内容
17.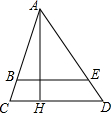 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.(1)求△ACD的周长;
(2)若AH=4.5cm,求△ABE的面积.
分析 (1)根据BE∥CD,得到△ABE∽△ACD,根据相似三角形的性质得到$\frac{AB}{AC}=\frac{AE}{AD}=\frac{BE}{CD}$,代入数据求得AD=$\frac{15}{2}$cm,CD=6cm,即可得到结果;
(2)根据三角形的面积公式即可得到结论.
解答 解:(1)∵BE∥CD,
∴△ABE∽△ACD,
∴$\frac{AB}{AC}=\frac{AE}{AD}=\frac{BE}{CD}$,
∴$\frac{4}{5}=\frac{6}{AD}=\frac{4.8}{CD}$,
∴AD=$\frac{15}{2}$cm,CD=6cm,
∴△ACD的周长=AC+AD+CD=5+$\frac{15}{2}$+6=$\frac{37}{2}$cm;
(2)∵AH是高,AH=4.5cm,CD=6cm,
∴S△ACD=$\frac{1}{2}$CD•AH=$\frac{1}{2}×6×4.5$$\frac{27}{2}$cm2.
点评 本题考查了相似三角形的判定和性质,三角形周长、面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
7.从分别标有号数1到10的10张卡片中,随意抽取一张,其号数为3的倍数的概率是( )
| A. | $\frac{7}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{10}$ |
 如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.
如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.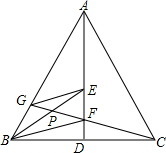 如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:
如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证: 在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$.
在△POQ中,∠POQ=120°,∠POQ的平分线OR交PQ于点R.求证:$\frac{1}{OR}$=$\frac{1}{OP}$+$\frac{1}{OQ}$. 用18m长的铝合金型材做一个形状如图所示的矩形窗框.做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用18m长的铝合金型材做一个形状如图所示的矩形窗框.做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少? 将含30°角的直角三角板的短直角边和含45°角的直角三角板的一条直角边如图放置,则∠1的度数为75度.
将含30°角的直角三角板的短直角边和含45°角的直角三角板的一条直角边如图放置,则∠1的度数为75度.