题目内容
9.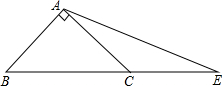 己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.
己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.(1)请在图中,用尺规作图的方法在射纸CB上找一点Q,使得∠QAC=α,(保留作图痕迹,不必证明).并直接写出∠AQB的大小;
(2)在(1)的条件下,证明:AP2+AQ2=(BP-CQ)2.
分析 (1)利用基本作图(作一个角等于已知角画出∠QAC=∠PAC;
(2)作∠BAM=α,如图,则∠BAM=∠CAQ,则可证明△ABM≌△ACQ得到BM=CQ,AM=AQ,所以BP-CQ=BP-BM=PM,再证明∠MAP=90°,然后利用勾股定理得到PM2=AP2+AM2,于是利用等线段代换即可得到结论.
解答 (1)解:如图,∠QAC为所作;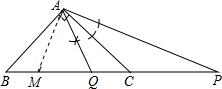
∵AB=AC=1,∠BAC=90°,
∴△ABC为等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠AQB=∠ACQ+∠QAC=45°+α;
(2)证明:作∠BAM=α,如图,则∠BAM=∠CAQ,
在△ABM和△ACQ中,
$\left\{\begin{array}{l}{∠B=∠ACQ}\\{AB=AC}\\{∠BAM=∠CAQ}\end{array}\right.$,
∴△ABM≌△ACQ,
∴BM=CQ,AM=AQ,
∴BP-CQ=BP-BM=PM,
∵∠BAM=∠PAC=α,
而∠BAC=90°,
∴∠MAP=90°,
在Rt△AMP中,PM2=AP2+AM2,
∴AP2+AQ2=(BP-CQ)2.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.解决(2)小题的关键是关键△ABM与△ACQ全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列计算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{(-3)^{3}}$=3 | D. | $\sqrt{(3.14-π)^{2}}$=π-3.14 |
4.下列各式是二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{m}$ | C. | $\sqrt{-16}$ | D. | $\root{3}{27}$ |
18.函数y=$\sqrt{3-x}$+$\frac{1}{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x<3 | C. | x≠3 | D. | x>3 |
 如图,在△ABC中,AC的垂直平分线交AB于点E,D为垂足,连接EC.若∠A=30°,则∠BEC=60°.
如图,在△ABC中,AC的垂直平分线交AB于点E,D为垂足,连接EC.若∠A=30°,则∠BEC=60°. 己知∠AOB=70°,根据语句画图,并填空
己知∠AOB=70°,根据语句画图,并填空