题目内容
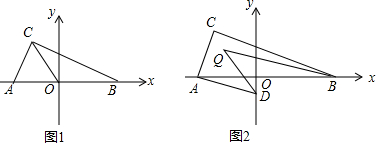
14.如图1,在平面直角坐标系中,已知A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.(1)求a,b的值;
(2)点M为坐标轴上一点,使△COM的面积是△ABC的面积的一半,求点M的坐标;
(3)如图2,过A作AD∥BC交y轴于D点,BQ平分∠ABC,DQ平分∠ADO,求∠DQB的度数.
分析 (1)根据非负性求出a,b的值;
(2)根据三角形的面积建立方程求出点M的坐标;
(3)利用平行线的性质,和整体思想求出角的度数.
解答 解:(1)∵|2a+b+1|+(a+2b-4)2=0,
∴2a+b+1=0,a+2b-4=0,
∴a=-2,b=3,
(2)由(1)有a=-2,b=3,
∴A(-2,0),B(3,0),
∴AB=5,
∴S△ABC=$\frac{1}{2}$AB×|yC|=$\frac{1}{2}$×5×2=5,
∵△COM的面积是△ABC的面积的一半,
∴S△COM=$\frac{5}{2}$,
①当点M在x轴上时,设M(m,0),
∴S△COM=$\frac{1}{2}$×OM×|yC|=$\frac{1}{2}$×|m|×2=$\frac{5}{2}$,
∴|m|=$\frac{5}{2}$,∴m=±$\frac{5}{2}$,
∴M(-$\frac{5}{2}$,0)或M($\frac{5}{2}$,O),
②当点M在y轴上时,
设M(0,n)
∴S△COM=$\frac{1}{2}$×OM×|xC|=$\frac{1}{2}$×|n|×1=$\frac{5}{2}$,
∴|n|=5,
∴n=±5,
∴M(0,-5)或M(0,5),
(3)过点Q作∥BC,
∴QM∥BC∥AD,
∴∠DQB=∠CBQ+∠ADQ=45°
点评 此题是坐标与图形题,主要考查绝对值和平方的非负性,三角形面积的应用,角的计算,解本题的关键是求出△ABC的面积.

练习册系列答案
相关题目
10. 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
2.下列代数运算正确的是( )
| A. | 2-3=-8 | B. | (2x2)3=8x6 | C. | x6÷x2=x3 | D. | x2+x3=2x5 |
6.下面的式子中正确的是( )
| A. | 3m-5m=-2 | B. | 5a+7b=7ab | C. | 3a2-2a2=2a | D. | 5xy2-6xy2=-xy2 |
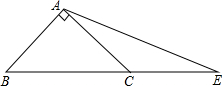 己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.
己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.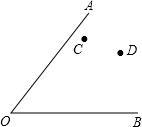 如图所示,点C、D是∠AOB内部的两点.
如图所示,点C、D是∠AOB内部的两点.