题目内容
2.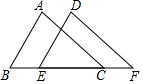 如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.
如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.求证:(1)△ABC≌△DEF;
(2)AB∥DE.
分析 (1)根据平行线的性质可得∠ACB=∠F,由BE=CF可得BC=EF.运用SAS证明△ABC与△DEF全等;
(2)根据两三角形全等得到∠B=∠DEF,利用同位角相等,证明出两直线平行.
解答 (1)证明:∵AC∥DF,
∴∠ACB=∠F,
∵BE=CF,
∴BC=EF,
∴在△ABC和△DEF中,
$\left\{\begin{array}{l}{AC=DF}\\{∠ACB=∠F}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF
∴∠B=∠DEF,
∴AB∥DE.
点评 本题考查了全等三角形的性质和判定.全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应角相等.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
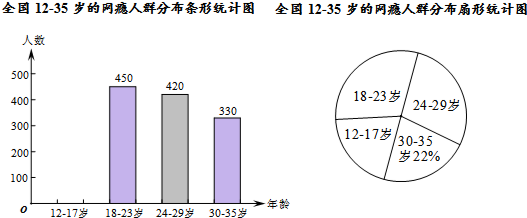
 如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.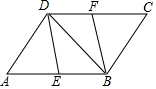 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.