题目内容
13.网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12-35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.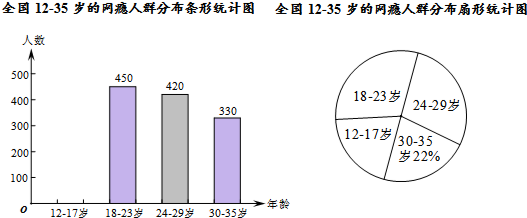
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了1500人,并请补全条形统计图;
(2)扇形统计图中18-23岁部分的圆心角的度数是108度;
(3)据报道,目前我国12-35岁“网瘾人数”约为2000万,请估计其中12-17岁的人数.
分析 (1)根据30-35岁的人数除以所占的百分比,可得调查的人数,由各年龄段的人数之和等于总人数求得12-17岁人数可不全条形图;
(2)根据18-23岁的人数除以抽查的人数乘以360°,可得答案;
(3)根据总人数乘以12-17岁的人数所占的百分比,可得答案.
解答 解:(1)这次抽样调查中调查的总人数为330÷22%=1500,
则12~17岁的人数为1500-(450+420+330)=300(人),
补全条形图如下: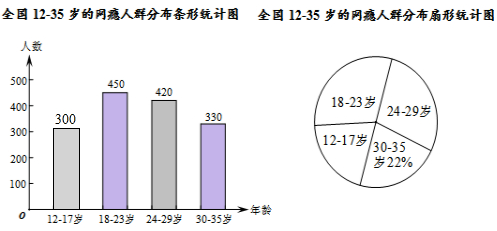
(2)扇形统计图中18-23岁部分的圆心角的度数是360°×$\frac{450}{1500}$=108°,
故答案为:108;
(3)2000×$\frac{300}{1500}$=400(万人),
答:估计其中12-17岁的人数为400万人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
5.某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每分钟收费b元,如果某人打一次该长途电话被收费m元,则这次长途电话的时间是( )
| A. | $\frac{m-a}{b}$分钟 | B. | $\frac{m}{a+b}$分钟 | C. | $\frac{m-a+b}{b}$分钟 | D. | $\frac{m-a-b}{b}$分钟 |
3.下列运算中,正确的是( )
| A. | a3+a3=2a6 | B. | a5-a3=a2 | C. | a2•a2=2a4 | D. | (a5)2=a10 |
 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.
如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数. 某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题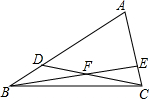 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72. 如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)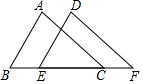 如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.
如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.