题目内容
14.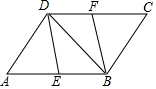 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.(1)求证:DE=FB;
(2)若AB=2AD=4,∠A=60°,求∠CBD的度数.
分析 (1)根据矩形的性质和已知证明DF=BE,AB∥CD,得到四边形DEBF是平行四边形,根据平行四边形的性质得到答案;
(2)证出△ADE为等边三角形,得出∠ADE=∠AED=60°,证出∠ADB=90°,由平行线的性质即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∵E、F分别是AB、CD的中点,
∴DE=EB
∴四边形DEBF是平行四边形
∴DE=FB;
(2)解:∵AB=2AD=4,
∴AD=AE=2
又∵∠A=60°,
∴△ADE为等边三角形
∴∠ADE=∠AED=60°,
又∵DE=AE=BE,
∴∠EBD=∠EDB=30°,
∴∠ADB=∠ADE+∠EDB=90°,
又AD∥BC,
∴∠CBD=∠ADB=90°.
点评 本题考查的是矩形的性质、平行四边形的判定和性质,掌握相关的判定定理和性质定理是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每分钟收费b元,如果某人打一次该长途电话被收费m元,则这次长途电话的时间是( )
| A. | $\frac{m-a}{b}$分钟 | B. | $\frac{m}{a+b}$分钟 | C. | $\frac{m-a+b}{b}$分钟 | D. | $\frac{m-a-b}{b}$分钟 |
6.下列四个点中,有三个点在同一反比例函数y=$\frac{k}{x}$的图象上,则不在这个函数图象上的点是( )
| A. | (5,1) | B. | (-1,5) | C. | (-3,-$\frac{5}{3}$) | D. | ($\frac{5}{3}$,3) |
3.下列运算中,正确的是( )
| A. | a3+a3=2a6 | B. | a5-a3=a2 | C. | a2•a2=2a4 | D. | (a5)2=a10 |
 如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.
如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.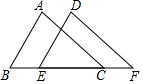 如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.
如图,点B、E、C、F在同一条直线上,AC∥DF,AC=DF,BE=CF.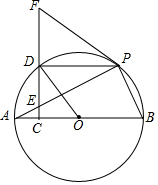 如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.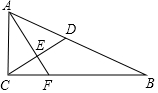 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.