题目内容
12.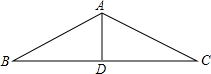 如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.(1)判断△ABD是否为直角三角形,并说明理由.
(2)求AC的长度.
分析 (1)先根据AD是BD上的中线求出BD的长,再根据勾股定理的逆定理判断出△ABD的形状为直角三角形;
(2)由(1)可判断△ADC为直角三角形,然后根据勾股定理即可求AC的长度.
解答 解:(1)△ABD是直角三角形,
理由:∵AD是BC边上的中线,
∴BD=DC=$\frac{1}{2}$BC=5$\sqrt{3}$,
在△ABD中,
∵AD2+BD2=52+(5$\sqrt{3}$)2=100=102=AB2,
∴△ABD是直角三角形,且∠ADB=90°;
(2)∵∠ADB=90°,
∴∠ADC=90°,
∴△ADC是直角三角形,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{5}^{2}+(5\sqrt{3})^{2}}$=10.
点评 此题考查了勾股定理及勾股定理的逆定理的应用,解题的关键是:由勾股定理的逆定理先判断△ABD是直角三角形.

练习册系列答案
相关题目
2. 如图是一根钢管的直观图,则它的主视图为( )
如图是一根钢管的直观图,则它的主视图为( )
 如图是一根钢管的直观图,则它的主视图为( )
如图是一根钢管的直观图,则它的主视图为( )| A. |  | B. |  | C. |  | D. |  |
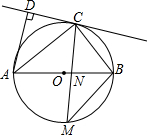 如图,AB是⊙O的直径,点C在⊙O上,AD和过C点的切线互相垂直,垂足为D.
如图,AB是⊙O的直径,点C在⊙O上,AD和过C点的切线互相垂直,垂足为D.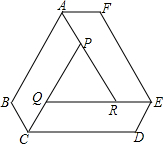 如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm
如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm 如图,长方形内小正方形的一条边在大正方形的一条边上,两个正方形的面积分别为3和4,那么阴影部分的面积是多少?
如图,长方形内小正方形的一条边在大正方形的一条边上,两个正方形的面积分别为3和4,那么阴影部分的面积是多少?