题目内容
14.(1)解方程:2x2+x=5;(2)已知x=$\frac{1}{\sqrt{3}-\sqrt{2}}$,求${(x+\frac{1}{x})}^{2}$+2(x+$\frac{1}{x}$)+2的值.
分析 (1)根据公式法求解即可;
(2)先化简x的值,再代入即可.
解答 解:(1)移项得,2x2+x-5=0;
∵a=2,b=1,c=-5,△=b2-4ac=1+40=41>0,
∴方程有两个不相等的实数根,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-1±\sqrt{41}}{4}$,
∴x1=$\frac{-1+\sqrt{41}}{4}$,x2=$\frac{-1-\sqrt{41}}{4}$;
(2)∵x=$\frac{1}{\sqrt{3}-\sqrt{2}}$,
∴x=$\sqrt{3}$+$\sqrt{2}$,
∴${(x+\frac{1}{x})}^{2}$+2(x+$\frac{1}{x}$)+2=(x+$\frac{1}{x}$+1)2+1=($\sqrt{3}$+$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$+1)2+1=(2$\sqrt{3}$+1)2+1=14+4$\sqrt{3}$.
点评 本题考查了分式的化简求值以及解一元二次方程,解方程的方法:直接开平方法、配方法、公式法、因式分解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
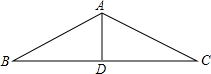 如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
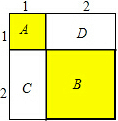 我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.