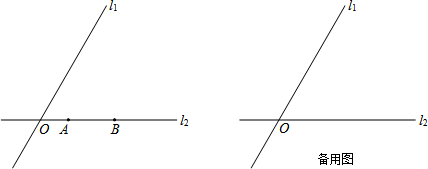题目内容
20.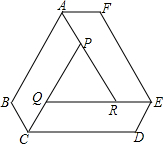 如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm
如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm(1)试帮工人师傅确定平行四边形木板各内角的度数、三角形木板各内角的度数及边长;
(2)求六边形桌面ABCDEF的面积(结果精确到0.1m2)
(参考数据:$\sqrt{3}$≈1.73,可使用科学计算器)
分析 (1)由平行四边形的性质就可以得出∠QPR=∠BAP.∠PQR=∠QCP,∠PRQ=∠REF.由全等形的性质就可以得出∠BAP=∠QCD=∠REF,CQ=BC,进而得出△PQR是等边三角形,由等边三角形的性质就可以求出结论;
(2)如图,过点P作PM⊥QR于M,过点Q作QN⊥CD于点N,由三角函数值就可以求出三角形的面积和一个平行四边形的面积,进而求出结论.
解答 解:(1)∵四边形ABCP是平行四边形,
∴AB∥CP,CP=AB=90,BC=AP=30°,
∴∠QPR=∠BAP.
同理:∠PQR=∠QCP,∠PRQ=∠REF.
∵平行四边形ABCP≌平行四边形CDEQ≌平行四边形EFRQ,
∴∠BAP=∠QCD=∠REF,CQ=BC=30,
∴∠QPR=∠PQR=∠PRQ,
∴△PQR是等边三角形,
∴∠QPR=∠PQR=∠PRQ=60°,PR=QR=PQ=CP-CQ=90-30=60,
∴∠BAP=∠QPR=60°,
∴∠APC=180°-∠QPR=120°,
∴平行四边形木板各内角的度数为60°、120°、60°、120°;三角形木板各内角的度数都为60°,边长都为60cm;
(2)如图,过点P作PM⊥QR于M,过点Q作QN⊥CD于点N.
∵PQ=60,∠PQR=60°,
∴PM=PQ•sin60°=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$.
同理:QN=15$\sqrt{3}$.
∴S△PQR=$\frac{1}{2}$QR•PM=$\frac{1}{2}×60×30\sqrt{3}$=900$\sqrt{3}$,
S平行四边形CDEQ=CD•QN=90×15$\sqrt{3}$=1350$\sqrt{3}$,
∴六边形桌面ABCDEF的面积为:3×1350$\sqrt{3}$+90$\sqrt{3}$=4140$\sqrt{3}$cm2≈0.7m2.
点评 本题考查了平行四边形的性质的运用,等边三角形的判定及性质的运用,全等形的性质的运用,平行四边形的面积公式的运用,三角形的面积公式的运用,解答时运用全等形的性质求解是关键.

 下列四幅图案中,能通过轴对称由图案1得到的是( )
下列四幅图案中,能通过轴对称由图案1得到的是( )| A. |  | B. |  | C. |  | D. |  |
| A. | x2+x3=x5 | B. | (x2)3=x6 | C. | 2x3÷x2=x | D. | 2x-1=$\frac{1}{2x}$ |
 已知线段AD上有B、C两点,说出图中总共有哪几条线段.
已知线段AD上有B、C两点,说出图中总共有哪几条线段.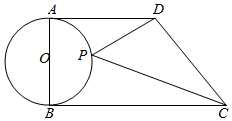 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )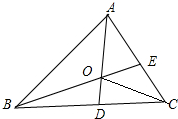 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断: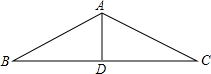 如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m. 如图,已知DE∥BC,∠1=∠2,那么∠B与∠C相等吗?为什么?
如图,已知DE∥BC,∠1=∠2,那么∠B与∠C相等吗?为什么?