题目内容
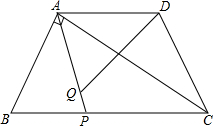 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°(1)求证:△ABP∽△DQA;
(2)当点P在BC上移动时,线段DQ的长度也随之变化,设PA=x,DQ=y.求y与x之间的函数关系式,并指出x的取值范围.
考点:等腰梯形的性质,相似三角形的判定与性质
专题:
分析:(1)根据已知求得∠DAQ=∠APB,∠B=∠AQD,即可求得结论;
(2)作AM⊥BC,DN⊥BC,垂足分别为M、N,即可求得BM=CN=1,然后根据30°角的直角三角形的性质即可求得AB=CD=2,根据相似三角形对应边成比例即可求得y与x之间的函数关系式,通过求得AC的长,即可求得x的取值范围.
(2)作AM⊥BC,DN⊥BC,垂足分别为M、N,即可求得BM=CN=1,然后根据30°角的直角三角形的性质即可求得AB=CD=2,根据相似三角形对应边成比例即可求得y与x之间的函数关系式,通过求得AC的长,即可求得x的取值范围.
解答:解:(1)∵AD∥BC,
∴∠DAQ=∠APB,
∵∠B=60°,∠AQD=60°,
∴∠B=∠AQD,
∴△ABP∽△DQA;
(2)作AM⊥BC,DN⊥BC,垂足分别为M、N,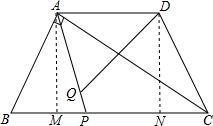
∵等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,
∴BM=CN=1,
∴AB=CD=2BM=2,
∵△ABP∽△DQA,
∴
=
,
设PA=x,DQ=y.
∴
=
,
∴y=
,
∵AD=DC=2,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∵∠B=∠BCD=60°,
∴∠ACB=30°
∴∠BAC=90°,
∴AC=
=
=2
,
∴x的取值范围为2<x<2
.
∴∠DAQ=∠APB,
∵∠B=60°,∠AQD=60°,
∴∠B=∠AQD,
∴△ABP∽△DQA;
(2)作AM⊥BC,DN⊥BC,垂足分别为M、N,

∵等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,
∴BM=CN=1,
∴AB=CD=2BM=2,
∵△ABP∽△DQA,
∴
| AD |
| AP |
| DQ |
| AB |
设PA=x,DQ=y.
∴
| 2 |
| x |
| y |
| 2 |
∴y=
| 4 |
| x |
∵AD=DC=2,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∵∠B=∠BCD=60°,
∴∠ACB=30°
∴∠BAC=90°,
∴AC=
| BC2-AB2 |
| 42-22 |
| 3 |
∴x的取值范围为2<x<2
| 3 |
点评:本题考查了等腰梯形的性质,30°角的直角三角形的性质,相似三角形的判定和性质,以及直角三角形的判定,勾股定理的应用等,求得AB的长是关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.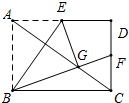 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.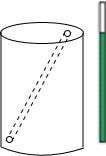 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)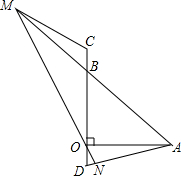 如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°.
如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°. 已知:如图,在△ABC中,AB=2,BC=4,D为BC边上一点,BD=1,求证:△ABC∽△DBA.
已知:如图,在△ABC中,AB=2,BC=4,D为BC边上一点,BD=1,求证:△ABC∽△DBA.