题目内容
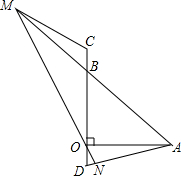 如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°.
如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°.考点:全等三角形的判定与性质
专题:证明题
分析:过B作BE⊥CD交MN于E,可证△AOD≌△OBE和△MBC≌△MBE,即可求得∠D=∠BEO和∠C=∠BEM,即可解题.
解答:解:过B作BE⊥CD交MN于E,

∵∠BOE=∠DON,∠BEO+∠BOE=90°,∠DON+∠ODN=90°,
∴∠BEO=∠ODN,
在△AOD和△OBE中,
,
∴△AOD≌△OBE(AAS),
∴OD=BE,∠D=∠BEO,
∵OB=OA,
∴∠OBA=45°,
∴∠MBE=∠MBC=45°,
在△MBC和△MBE中,
,
∴△MBC≌△MBE(SAS),
∴∠C=∠BEM,
∴∠C+∠D=∠BEM+∠BEO=180°.

∵∠BOE=∠DON,∠BEO+∠BOE=90°,∠DON+∠ODN=90°,
∴∠BEO=∠ODN,
在△AOD和△OBE中,
|
∴△AOD≌△OBE(AAS),
∴OD=BE,∠D=∠BEO,
∵OB=OA,
∴∠OBA=45°,
∴∠MBE=∠MBC=45°,
在△MBC和△MBE中,
|
∴△MBC≌△MBE(SAS),
∴∠C=∠BEM,
∴∠C+∠D=∠BEM+∠BEO=180°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题运用转化思维求解是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
若|x+1|+(y-2)2=0,则x2+y2=( )
| A、3 | B、5 | C、-1 | D、-5 |
下列说法正确的有( )
| A、优弧的长一定大于劣弧的长 |
| B、以圆心为端点的线段是半径 |
| C、半径相等的两个半圆是等弧 |
| D、不同的圆中,就不可能有相等的弦长 |
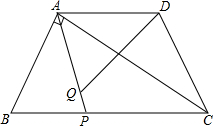 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60° 如图,△ABC中,AB=AC,AB⊥AC,D为AC的中点,AE⊥BD于E,CF⊥BD于F,求证:BE=2CF.
如图,△ABC中,AB=AC,AB⊥AC,D为AC的中点,AE⊥BD于E,CF⊥BD于F,求证:BE=2CF.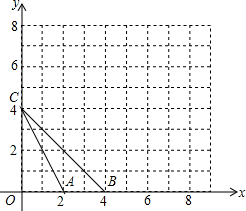 如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标.
如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标. 如图,△ABC中,∠B=∠ACB,CD是高,求证:∠BCD=
如图,△ABC中,∠B=∠ACB,CD是高,求证:∠BCD=