题目内容
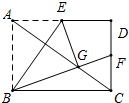 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线,首先证明△ADG是直角三角形,然后证明△DEF≌△GED,借助直角三角形的性质问题即可解决.
解答:证明: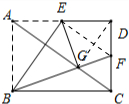 如图所示,连接EF,DG,
如图所示,连接EF,DG,
由题意知:AE=GE,∠BGE=∠BAE=90°;又E是AD中点,
∴GE=AE=DE;
∴△ADG是直角三角形,
∴∠DGC=∠AGD=90°;
在△DEF与△GED中,
,
∴△DEF≌△GED(HL),
∴GF=DF,
∴∠DGF=∠GDF,
∴∠CGF=∠GCF,
∴GF=CF,
∴DF=CF,
即点F是CD的中点.
 如图所示,连接EF,DG,
如图所示,连接EF,DG,由题意知:AE=GE,∠BGE=∠BAE=90°;又E是AD中点,
∴GE=AE=DE;
∴△ADG是直角三角形,
∴∠DGC=∠AGD=90°;
在△DEF与△GED中,
|
∴△DEF≌△GED(HL),
∴GF=DF,
∴∠DGF=∠GDF,
∴∠CGF=∠GCF,
∴GF=CF,
∴DF=CF,
即点F是CD的中点.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质准确找出命题中隐含的等量关系,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
式子
在实数范围内有意义,则x的取值范围是( )
| 3-2x |
A、x>
| ||
B、x≤
| ||
C、x≥
| ||
D、x≠
|
下列说法正确的有( )
| A、优弧的长一定大于劣弧的长 |
| B、以圆心为端点的线段是半径 |
| C、半径相等的两个半圆是等弧 |
| D、不同的圆中,就不可能有相等的弦长 |
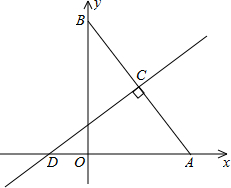 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-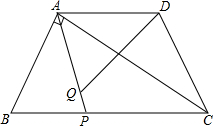 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°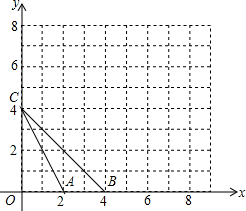 如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标.
如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标.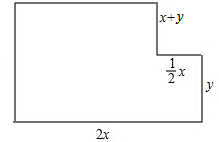 为了提高业主的宜居环境,某移民小区规划修建一个休闲场所(平面图形如图所示).
为了提高业主的宜居环境,某移民小区规划修建一个休闲场所(平面图形如图所示).