题目内容
已知：如图，在△ABC中，AB=2，BC=4，D为BC边上一点，BD=1，求证：△ABC∽△DBA．考点：相似三角形的判定
专题：证明题
分析：由题意得到两边对应比例，且夹角相等，利用两边对应成比例且夹角相等的三角形相似即可得证．
解答：证明：∵在△ABC中，AB=2，BC=4，BD=1，
∴
=
=2，
∵∠ABD=∠CBA=90°，
∴△ABC∽△DBA．
∴
| AB |
| BD |
| BC |
| AB |
∵∠ABD=∠CBA=90°，
∴△ABC∽△DBA．
点评：此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．
练习册系列答案
相关题目
式子
在实数范围内有意义，则x的取值范围是（ ）
| 3-2x |
A、x＞
| ||
B、x≤
| ||
C、x≥
| ||
D、x≠
|
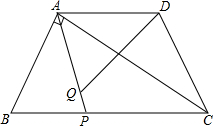如图，等腰梯形ABCD中，AB=CD，AD∥BC，AD=2，BC=4，∠B=60°，如果P是BC上一点，Q是AP上一点，且∠AQD=60°
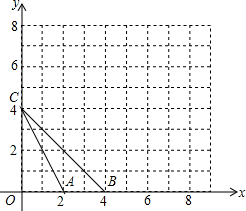如图，在平面直角坐标系中，△ABC的顶点坐标为A（2，0）、B（4，0）、C（0，4），将各顶点的横坐标、纵坐标都乘2，得相应的点A′、B′、C′的坐标．
如图，△ABC中，∠B=∠ACB，CD是高，求证：∠BCD=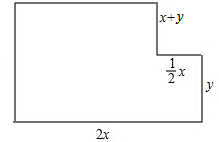
为了提高业主的宜居环境，某移民小区规划修建一个休闲场所（平面图形如图所示）．