题目内容
△ABC是直径为10cm的圆的内接等腰三角形,△ABC的底边BC=8cm,则S△ABC= cm2.
考点:三角形的外接圆与外心,等腰三角形的性质
专题:分类讨论
分析:已知△ABC是等腰三角形,根据等腰三角形的性质,若过A作底边BC的垂线AD,则AD所在直线必过圆心O;在Rt△OBD中,由勾股定理可求出OD的长,进而可求出△AOB的面积.需注意本题的△ABC分锐角和钝角三角形两种情况.
解答: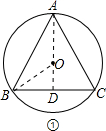 解:(1)如图①:
解:(1)如图①:
过A作AD⊥BC于D,则AD必过点O,连接OB;
Rt△OBD中,OB=5cm,BD=4cm;
由勾股定理,得:OD=
=3cm;
则AD=OA+OD=8cm,
S△ABC=
BC•AD=32(cm2);
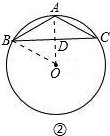
(2)如图②:同(1)可求得OD=3cm,
则AD=OA-OD=2cm,
S△ABC=
BC•AD=8(cm2).
所以△ABC的面积是32或8平方厘米.
故答案为32或8.
 解:(1)如图①:
解:(1)如图①:过A作AD⊥BC于D,则AD必过点O,连接OB;
Rt△OBD中,OB=5cm,BD=4cm;
由勾股定理,得:OD=
| OB2-BD2 |
则AD=OA+OD=8cm,
S△ABC=
| 1 |
| 2 |

(2)如图②:同(1)可求得OD=3cm,
则AD=OA-OD=2cm,
S△ABC=
| 1 |
| 2 |
所以△ABC的面积是32或8平方厘米.
故答案为32或8.
点评:本题考查了三角形的外接圆,用到的知识点是等腰三角形的性质和勾股定理等知识的综合应用,关键是根据题意,画出图形.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列说法正确的有( )
| A、优弧的长一定大于劣弧的长 |
| B、以圆心为端点的线段是半径 |
| C、半径相等的两个半圆是等弧 |
| D、不同的圆中,就不可能有相等的弦长 |
 如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.
如图,楼高AB为26米,从楼顶A处测得旗杆顶C的俯角为60°,又从距离楼底B处4m的一窗口E处测得旗杆顶C的仰角为45°,求旗杆CD的高.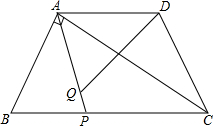 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60° 如图,△ABC中,AB=AC,AB⊥AC,D为AC的中点,AE⊥BD于E,CF⊥BD于F,求证:BE=2CF.
如图,△ABC中,AB=AC,AB⊥AC,D为AC的中点,AE⊥BD于E,CF⊥BD于F,求证:BE=2CF. 如图,四边形ABCD中,AC⊥BD,求证:BC+AD>AB+CD.
如图,四边形ABCD中,AC⊥BD,求证:BC+AD>AB+CD.