题目内容
 如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.考点:射影定理,相似三角形的判定与性质
专题:证明题
分析:根据相似三角形的判定方法证明Rt△ABD∽Rt△ACB得到AB:AC=AD:AB,再利用比例性质可得AB2=AD•AC;证明Rt△ABD∽Rt△BCD得到BD:CD=AD:BD,
利用比例性质可得BD2=AD•DC.
利用比例性质可得BD2=AD•DC.
解答:证明:∵BD⊥AC,
∴∠ADB=∠CDB=90°,
∵∠BAD=∠CAB,
∴Rt△ABD∽Rt△ACB,
∴AB:AC=AD:AB,
∴AB2=AD•AC;
∵∠A+∠ABD=90°,∠DBC+∠ABD=90°,
∴∠A=∠DBC,
∴Rt△ABD∽Rt△BCD,
∴BD:CD=AD:BD,
∴BD2=AD•DC.
∴∠ADB=∠CDB=90°,
∵∠BAD=∠CAB,
∴Rt△ABD∽Rt△ACB,
∴AB:AC=AD:AB,
∴AB2=AD•AC;
∵∠A+∠ABD=90°,∠DBC+∠ABD=90°,
∴∠A=∠DBC,
∴Rt△ABD∽Rt△BCD,
∴BD:CD=AD:BD,
∴BD2=AD•DC.
点评:本题考查了射影定理:在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
下列各式中运算错误的是( )
| A、-xy+xy=0 |
| B、4x-2x=2x |
| C、5x2y-6xy2=-1 |
| D、2xy-yx=xy |
若|x+1|+(y-2)2=0,则x2+y2=( )
| A、3 | B、5 | C、-1 | D、-5 |
式子
在实数范围内有意义,则x的取值范围是( )
| 3-2x |
A、x>
| ||
B、x≤
| ||
C、x≥
| ||
D、x≠
|
下列说法正确的有( )
| A、优弧的长一定大于劣弧的长 |
| B、以圆心为端点的线段是半径 |
| C、半径相等的两个半圆是等弧 |
| D、不同的圆中,就不可能有相等的弦长 |
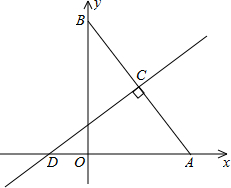 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-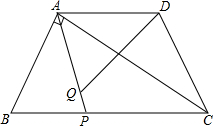 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60° 如图,△ABC中,∠B=∠ACB,CD是高,求证:∠BCD=
如图,△ABC中,∠B=∠ACB,CD是高,求证:∠BCD=