题目内容
如图，AB是⊙O直径，弦CD与AB相交于点E，∠ACD=52°，∠ADC=26°．求∠CEB的度数．考点：圆周角定理
专题：
分析：首先连接BD，由AB是⊙O直径，根据直径所对的圆周角是直角，可得∠ADB=90°，又由圆周角定理，可求得∠B的度数，继而求得∠BAD的度数，然后由三角形内角和定理，求得答案．
解答：
解：连接BD，
∵AB是⊙O直径，
∴∠ADB=90°，
∵∠B=∠ACD=52°，
∴∠BAD=90°-∠B=38°，
∵∠ADC=26°，
∴∠CEB=∠AED=180°-∠BAD-∠ADC=116°．
解：连接BD，∵AB是⊙O直径，
∴∠ADB=90°，
∵∠B=∠ACD=52°，
∴∠BAD=90°-∠B=38°，
∵∠ADC=26°，
∴∠CEB=∠AED=180°-∠BAD-∠ADC=116°．
点评：此题考查了圆周角定理．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
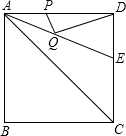如图，正方形ABCD的边长为8，∠DAC的平分线交DC于点E．若点P，Q分别是AD和AE上的动点，则DQ+PQ的最小值是（ ）
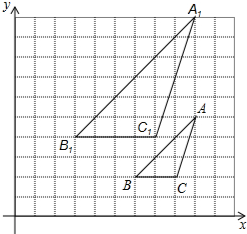如图，已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点为格点．若△ABC与△A1B1C1是位似图形，且顶点都在格点上，请你画出位似中心点O，并写出位似中心的坐标（保留作图痕迹）．当x为任意实数时，下列分式一定有意义的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
