题目内容
 某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.
某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.(1)这批柑橘在三、月份售出的平均售价分别是多少?
(2)请求出销售柑橘的总收益w(元)与销售时间x(月)之间的函数关系式,并求出几月份全部售出收益最大?最大收益是多少?
(3)4月20日四川雅安芦山县发生7.0级地震,全国各地纷纷伸出援助之手,该水果种植户决定将这批柑橘在4月份全部售出,并将所得收益全部均给灾区,那么它可为灾区筹得捐款多少元?
考点:二次函数的应用
专题:
分析:(1)设所求直线的解析式为y=kx+b,由待定系数法求出一次函数的解析式,在当x=3或x=4代入解析式求出其解即可;
(2)根据总收益=销售时间×销售量-保存费就可以得出w(元)与销售时间x(月)之间的函数关系式;
(3)当x=4代入(2)的解析式求出结论即可.
(2)根据总收益=销售时间×销售量-保存费就可以得出w(元)与销售时间x(月)之间的函数关系式;
(3)当x=4代入(2)的解析式求出结论即可.
解答:解:(1)设所求直线的解析式为y=kx+b,由题意,得
,
解得:
,
∴y=0.2x+2.
当x=3时,y=0.2×3+2=2.6元
当x=4时,y=0.2×4+2=2.8元.
答:这批柑橘在三、四月份售出的平均售价分别是2.6元,2.8元;
(2)由题意,得
W=(4000-200x)(0.2x+2-0.02),
=-40x2+404x+7920,
∴a=-40<0
∴当x=-
=
=5.05≈5时,W最大=-40×52+404×5+7920=8940.
答:五月份卖出收益最大为8940元;
(3)当x=4时,
W=-40×42+404×4+7920=8896元.
答:它可为灾区筹得捐款8896元.
|
解得:
|
∴y=0.2x+2.
当x=3时,y=0.2×3+2=2.6元
当x=4时,y=0.2×4+2=2.8元.
答:这批柑橘在三、四月份售出的平均售价分别是2.6元,2.8元;
(2)由题意,得
W=(4000-200x)(0.2x+2-0.02),
=-40x2+404x+7920,
∴a=-40<0
∴当x=-
| b |
| 2a |
| 404 |
| -40×2 |
答:五月份卖出收益最大为8940元;
(3)当x=4时,
W=-40×42+404×4+7920=8896元.
答:它可为灾区筹得捐款8896元.
点评:本题考查了运用待定系数法求一次函数的解析式的运用,销售问题的数量关系的运用,二次函数的性质的运用,由自变量的值求函数值的运用.解答时求出函数解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
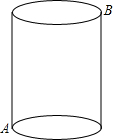 如图,一圆柱体木块高5cm,底面半径
如图,一圆柱体木块高5cm,底面半径
 如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为
如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为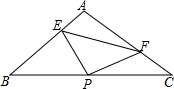 如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.
如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.