题目内容
如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且
+|BC-6|=0,点P、Q分别是边AD、AB上的动点.
(1)求BD的长;
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
| AB-4 |

(1)求BD的长;
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
考点:四边形综合题
专题:
分析:(1)由条件可求得AB=4,BC=6,由勾股定理可求出BD的长;
(2)①由题可知只能有∠QPC为直角,当PQ=PC时,可证得Rt△PDC≌Rt△QAP,可求得AP的长;②分PC=EC、PC=PE和PE=EC三种情况分别利用等腰三角形的性质和勾股定理求解即可.
(2)①由题可知只能有∠QPC为直角,当PQ=PC时,可证得Rt△PDC≌Rt△QAP,可求得AP的长;②分PC=EC、PC=PE和PE=EC三种情况分别利用等腰三角形的性质和勾股定理求解即可.
解答:解:
(1)如图1,连接BD,
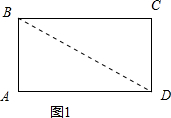
∵
+|BC-6|=0,
∴AB=4,BC=6,
则在Rt△ABD中,由勾股定理可求得BD=
=2
;
(2)①能,AP=4,理由如下:
如图2,由图形可知∠PQC和∠PCQ不可能为直角,所以只有∠QPC=90°,则∠QPA+∠CPD=∠PCD+∠CPD,
∴∠QPA=∠PCD,
当PQ=PC时,
在Rt△APQ和Rt△DCP中
∴△APQ≌△DCP(AAS),
∴AP=CD=4,
故在P、Q运动中是否能使△CPQ成为等腰直角三角形,此时AP=4;
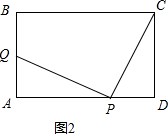
②当PC=EC=5时,在Rt△PCD中,CD=4,PC=EC=5,由勾股定理可求得PD=3,所以AP=AB-PD=3,
当PC=PE=5时,如图3,过P作PF⊥BC交BC于点F,则FC=EF=PD=
EC=2.5,所以AP=AB-PD=6-2.5=3.5,
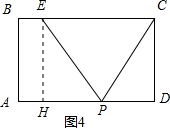
当PE=EC=5时,如图4,过E作EH⊥AD于点H,由可知AH=BE=1,在Rt△EHD中,EH=AB=4,EP=5,由勾股定理可得HP=3,所以AP=AH+PH=1+3=4,
综上可知当△EPC为等腰三角形时,求出PA的长为3、3.5或4.
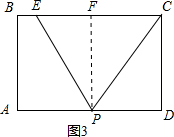
(1)如图1,连接BD,

∵
| AB-4 |
∴AB=4,BC=6,
则在Rt△ABD中,由勾股定理可求得BD=
| 42+62 |
| 13 |
(2)①能,AP=4,理由如下:
如图2,由图形可知∠PQC和∠PCQ不可能为直角,所以只有∠QPC=90°,则∠QPA+∠CPD=∠PCD+∠CPD,
∴∠QPA=∠PCD,
当PQ=PC时,
在Rt△APQ和Rt△DCP中
|
∴△APQ≌△DCP(AAS),
∴AP=CD=4,
故在P、Q运动中是否能使△CPQ成为等腰直角三角形,此时AP=4;

②当PC=EC=5时,在Rt△PCD中,CD=4,PC=EC=5,由勾股定理可求得PD=3,所以AP=AB-PD=3,
当PC=PE=5时,如图3,过P作PF⊥BC交BC于点F,则FC=EF=PD=
| 1 |
| 2 |
当PE=EC=5时,如图4,过E作EH⊥AD于点H,由可知AH=BE=1,在Rt△EHD中,EH=AB=4,EP=5,由勾股定理可得HP=3,所以AP=AH+PH=1+3=4,
综上可知当△EPC为等腰三角形时,求出PA的长为3、3.5或4.


点评:本题主要考查矩形的性质及全等三角形的判定和性质、等腰三角形的性质的综合应用,在(2)①中判断出只有PQ=PC一种情况、②中分三种情况进行讨论求解是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
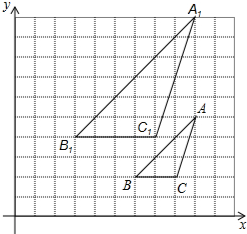 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,请你画出位似中心点O,并写出位似中心的坐标(保留作图痕迹).
如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,请你画出位似中心点O,并写出位似中心的坐标(保留作图痕迹).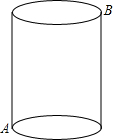 如图,一圆柱体木块高5cm,底面半径
如图,一圆柱体木块高5cm,底面半径 如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=4,直线y=2x-4经过点C,交y轴于点G.
如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=4,直线y=2x-4经过点C,交y轴于点G.
 如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为
如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为