题目内容
2. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 1或$\frac{7}{4}$ | D. | 1或$\frac{3}{2}$ |
分析 先根据圆周角定理得到∠ACB=90°,再利用含30度的直角三角形三边的关系得到AB=2BC=4,则BF=$\frac{1}{2}$BC=1,然后分类讨论:当∠BFE=90°时,由于∠B=60°,利用含30度的直角三角形三边的关系得到BE=2BF=2,则AE=AB-BE=2,可计算出t=1(s);同理可得当∠BEF=90°时,AE=AB-BE=$\frac{7}{2}$,此时t=$\frac{7}{4}$(s).
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴AB=2BC=4,
∵F是弦BC的中点,
∴BF=$\frac{1}{2}$BC=1,
当∠BFE=90°时,∠B=60°,BE=2BF=2,则AE=AB-BE=2,此时t=$\frac{2}{2}$=1(s);
当∠BEF=90°时,∠B=60°,BE=$\frac{1}{2}$BF=$\frac{1}{2}$,则AE=AB-BE=$\frac{7}{2}$,此时t=$\frac{\frac{7}{2}}{2}$=$\frac{7}{4}$(s),
综上所述,t的值为1s或$\frac{7}{4}$s.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
13.有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个三角形的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{10}$ |
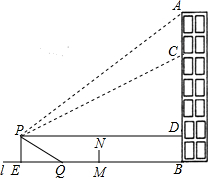 如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内. 在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.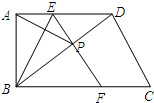 如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.
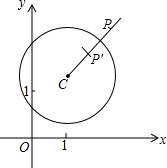 在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.