题目内容
10. 在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
分析 根据等边对等角可得∠B=∠BCD,然后利用等角的余角相等求出∠A=∠ACD,然后根据等角对等边可得AD=CD,从而得到AD=CD=BD,再求解即可.
解答 解:∵CD=BD,
∴∠B=∠BCD,
∵∠C=90°,
∴∠B+∠A=90°,
∠ACD+∠BCD=90°,
∴∠A=∠ACD,
∴AD=CD,
∴AD=CD=BD,
∵AB=10,
∴CD=$\frac{1}{2}$×10=5.
故答案为:5.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边对等角的性质,等角对等边的性质以及等角的余角相等的性质,熟记各性质是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
20.现有点数为2,3,4,5的四张扑克牌,背面朝上洗匀,然后从中任意抽取从中任意抽取两张,这两张牌上的数字之和为偶数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
2. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )
 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 1或$\frac{7}{4}$ | D. | 1或$\frac{3}{2}$ |
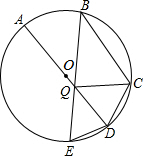 如图,已知A、B、C、D是⊙O上四点,点E在弧AD上,连接BE交AD于点Q,若∠AQE=∠EDC,∠CQD=∠E,求证:AQ=BC.
如图,已知A、B、C、D是⊙O上四点,点E在弧AD上,连接BE交AD于点Q,若∠AQE=∠EDC,∠CQD=∠E,求证:AQ=BC.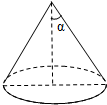 如图,圆锥的底面半径为5cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则sinα的值为$\frac{5}{11}$.
如图,圆锥的底面半径为5cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则sinα的值为$\frac{5}{11}$.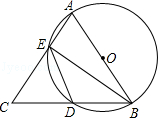 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE. 如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).
如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0). 如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.
如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.