题目内容
14．写一个经过点（0，2），且y随x增大而增大的一次函数y=x+2（答案不唯一）．分析 首先可由y随x的增大而增大确定x的系数k＞0，再根据函数图象经过点（0，2），写出符合题意的函数表达式即可．
解答 解：设一次函数的解析式为y=kx+b．
∵y随x的增大而增大，
∴k＞0．
∵函数图象需要经过点（0，2），
∴b=2，
∴函数表达式可以是y=x+2．
故答案为：y=x+2（答案不唯一）．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
4．小红和其他2名同学排成一排拍照，则小红排在正中间的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
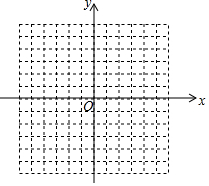如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点（即这些小正方形的顶点）上，且它们的坐标分别是A（2，-3），B（5，-1），C（-1，3），结合所给的平面直角坐标系，解答下列问题：
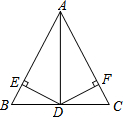如图，在△ABC中，AB=AC，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F，对于下列结论：①AD⊥BC；②AE=AF；③AD上任意一点到AB，AC的距离相等；④AD上任意一点到点B，点C的距离相等．其中正确结论的个数是（ ）
9．一个三角形三个内角的度数之比为3：4：5，这个三角形一定是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 等腰三角形 |
19．将函数y=$\frac{1}{2}$x2-x化为y=a（x-m）2+k的形式，得（ ）
| A． | y=$\frac{1}{2}$（x-1）2-$\frac{1}{2}$ | B． | y=$\frac{1}{2}$（x-$\frac{1}{4}$）2+$\frac{1}{32}$ | C． | y=$\frac{1}{2}$（x-1）2+$\frac{1}{2}$ | D． | y=$\frac{1}{2}$（x-$\frac{1}{4}$）2-$\frac{1}{32}$ |
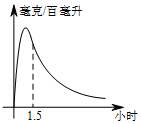实验数据显示：一般成人喝半斤低度白酒后，1.5小时内（包括1.5小时）其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x表示，1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）表示（如图所示）
3．己知△ABC中，∠C=Rt∠，若AC=$\sqrt{3}$，BC=1，则sinA的值是（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |