题目内容
19.将函数y=$\frac{1}{2}$x2-x化为y=a(x-m)2+k的形式,得( )| A. | y=$\frac{1}{2}$(x-1)2-$\frac{1}{2}$ | B. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2+$\frac{1}{32}$ | C. | y=$\frac{1}{2}$(x-1)2+$\frac{1}{2}$ | D. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2-$\frac{1}{32}$ |
分析 利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答 解:∵y=$\frac{1}{2}$x2-x=$\frac{1}{2}$(x2-2x+1)-$\frac{1}{2}$=$\frac{1}{2}$(x-1)2-$\frac{1}{2}$,
故选A.
点评 本题考查了二次函数的性质及二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
10.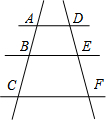 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )| A. | $\frac{9}{2}$ | B. | 2 | C. | $\frac{7}{2}$ | D. | 4 |
7.在Rt△ABC中,已知∠C=90°,AC=3,AB=4,则tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
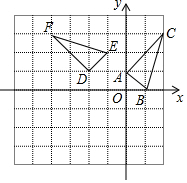 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0).
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0). 如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.
如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.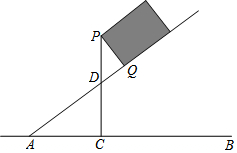 一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.
一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.