题目内容
16.提出问题:(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
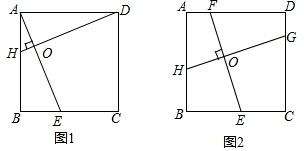
分析 (1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;
(2)将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO.
在△ABE和△DAH中
$\left\{\begin{array}{l}{∠BAE=∠HDA}\\{AB=AD}\\{∠B=∠HAD}\end{array}\right.$,
∴△ABE≌△DAH(ASA),
∴AE=DH;
(2)解:EF=GH.
理由:如图所示:
将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.
∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,所以EF=GH.
点评 本题考查了全等三角形的判定与性质、正方形的性质等知识,熟练利用全等三角形的判定方法得出全等三角形是解题关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
7.在?ABCD中,BD、AC是对角线,下列结论不正确的是( )
| A. | 当AB=BC时,?ABCD是菱形 | B. | 当∠ABC=90°时,?ABCD是矩形 | ||
| C. | 当AC⊥BD时,?ABCD是菱形 | D. | 当AC=BD时,?ABCD是正方形 |
6.4的平方根是( )
| A. | 2 | B. | ±2 | C. | -2 | D. | 不存在 |

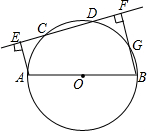 如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.