题目内容
6.若2a=3b=6c,求证:ab=ac+bc.分析 根据积的乘方,可得指数相同的幂的乘法,根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得相同的幂.根据同底数的幂相同,可得指数相同.
解答 证明:设2a=3b=6c=k,
则 6ab=2ab×3ab=(2a)b×(3b)a=kb•ka=ka+b,
6ac+bc=(6c)a+b=ka+b
所以6ab=6ac+bc,
所以ab=ac+bc.
点评 本题考查了幂的乘方与积得乘方,先由积的乘方化成同底数幂的乘法,再由幂的乘方化成同底数的相同的幂.

练习册系列答案
相关题目
 如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?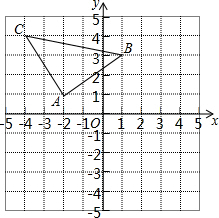 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).
如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).