题目内容
8.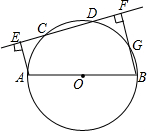 如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
分析 根据直径所对的圆周角是直角得到BF⊥AG,根据两条平行线所夹的弧相等得到答案.
解答  证明:连接AG,
证明:连接AG,
∵AB是⊙O的直径,
∴BF⊥AG,又BF⊥CD,
∴AG∥EF,
∴$\widehat{AC}$=$\widehat{DG}$.
点评 本题考查的是圆周角定理和垂径定理的应用,掌握直径所对的圆周角是直角和两条平行线所夹的弧相等是解题的关键.

练习册系列答案
相关题目
13.与$\sqrt{6}$最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.抛物线y=-2(x+6)2+5的顶点坐标是( )
| A. | (6,5) | B. | (-6,5) | C. | (6,-5) | D. | (-2,5) |
18.已知点A(-2,y1)、B(1,y2)、C(4,y3)都在函数y=x2-4x-5的图象上,则比较y1、y2、y3的大小正确的是( )
| A. | y2<y3<y1 | B. | y3<y1<y2 | C. | y1<y3<y2 | D. | y2<y1<y3 |
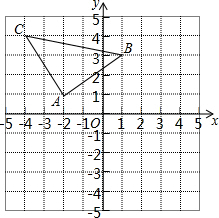 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).
如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).
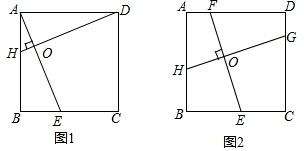
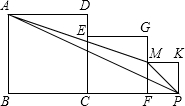 如图所示,三个正方形边长分别为1,2,3,求三角形AMP的面积.
如图所示,三个正方形边长分别为1,2,3,求三角形AMP的面积.