Question

11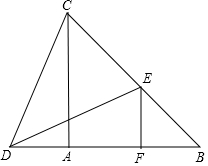．如图，在△ABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=CD，EF∥AC，交AB于点F．
（1）求证：∠ACD=∠BDE．
（2）求证：EF=AD．

Answer 1

分析 （1）先根据等边对等角，得出∠1+∠2=∠3，再根据三角形外角性质，得出∠3=∠4+∠5，进而得到∠1+∠2=∠4+∠5，最后根据根据∠2=∠5，即可得出结论；
（2）先根据平行线的性质，得出∠7=∠6，再根据AAS判定△CDA≌△DEF，即可得出EF=AD．

解答 证明：（1）∵DC=DE，
∴∠1+∠2=∠3，
又∵∠3=∠4+∠5，
∴∠1+∠2=∠4+∠5，
由AC=AB可得：∠2=∠5，
∴∠1=∠4，
即∠ACD=∠BDE；

（2）∵AC∥EF，
∴∠7=∠6
在△CDA和△DEF中，
$\left\{\begin{array}{l}{∠7=∠6}\\{∠1=∠4}\\{CD=DE}\end{array}\right.$，
∴△CDA≌△DEF（AAS），
∴AD=EF．

点评 本题主要考查了全等三角形的判定与性质、等腰三角形的性质以及三角形外角性质的综合应用，解题时注意：两角及其中一个角的对边对应相等的两个三角形全等，全等三角形的对应边相等．