题目内容
1. 已知:如图,在△ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M.
已知:如图,在△ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M.(1)求证:BE=CD;
(2)求∠BMC的度数.
分析 (1)由等边三角形不难得出△DAC≌△BAE;
(2)△DAC≌△BAE得出∠ACD=∠AEB,再利用角之间的转化,进而可得出结论.
解答 证明:(1)∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠CAE=60°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△DAC与△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AE=AC}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
(2)∵△DAC≌△BAE,
∴∠ACD=∠AEB,
∠DME=∠BEC+∠ECM=∠BEC+∠ECA+∠ACD=120°,
∴∠BMC=120°.
点评 本题主要考查了等边三角形的性质以及全等三角形的判定及性质,能够熟练运用其性质求解一些简单的计算问题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
12.已知函数y=7x|m|+m-1是正比例函数,则m的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
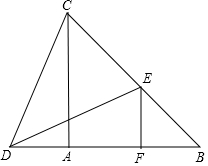 如图,在△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=CD,EF∥AC,交AB于点F.
如图,在△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=CD,EF∥AC,交AB于点F. 某自行车厂生产产量如下图表所示,5月份产量比4月份减少了10%,且6、7月份增长率均为x,求增长的百分率.
某自行车厂生产产量如下图表所示,5月份产量比4月份减少了10%,且6、7月份增长率均为x,求增长的百分率.
 如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.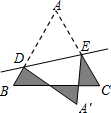 等腰△ABC的腰为6,底为5,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,求阴影部分图形的周长.
等腰△ABC的腰为6,底为5,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,求阴影部分图形的周长.