题目内容
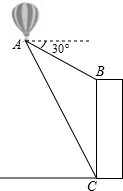 如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.
如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.考点:解直角三角形的应用-仰角俯角问题
专题:
分析:先过A作BC的垂线,设垂足为D,在Rt△ACD中,利用∠CAD的正切函数求出邻边AD的长,再在Rt△ABD中,利用已知角的三角函数求出BD的长,再由BC=CD-BD即可求出楼的高度.
解答: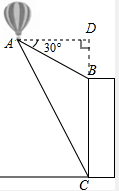 解:作AD⊥CB,交CB的延长线于D点,
解:作AD⊥CB,交CB的延长线于D点,
则∠CDA=90°,∠CAD=60°,∠BAD=30°,CD=180米,
在Rt△ACD中,tan∠CAD=
,
∴AD=
=
=60
,
在Rt△ABD中,tan∠BAD=
,
∴BD=AD•tan30°=60
×
=60,
∴BC=CD-BD=180-60=120.
答:这栋大楼的高为120米.
 解:作AD⊥CB,交CB的延长线于D点,
解:作AD⊥CB,交CB的延长线于D点,则∠CDA=90°,∠CAD=60°,∠BAD=30°,CD=180米,
在Rt△ACD中,tan∠CAD=
| CD |
| AD |
∴AD=
| CD |
| tan60° |
| 180 | ||
|
| 3 |
在Rt△ABD中,tan∠BAD=
| BD |
| AD |
∴BD=AD•tan30°=60
| 3 |
| ||
| 3 |
∴BC=CD-BD=180-60=120.
答:这栋大楼的高为120米.
点评:此题考查了解直角三角形的应用,用到的知识点是俯角的定义、特殊角的三角函数值,关键是作出辅助线,构造直角三角形.

练习册系列答案
相关题目
等腰三角形一腰上的高与腰长之比为1:2,则等腰三角形顶角的度数为( )
| A、60° |
| B、120° |
| C、30°或150° |
| D、60°或120° |
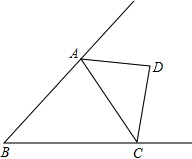 如图,点D是△ABC的两外角平分线的交点,下列说法:
如图,点D是△ABC的两外角平分线的交点,下列说法:①AD=CD; ②点D到AB、BC所在直线的距离相等;
③点D到三边AB、BC、AC所在直线的距离相等;④点D在∠B的平分线上.
其中正确的是( )
| A、②④④ | B、①②④ |
| C、②③④ | D、①②③④ |
下列根式是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
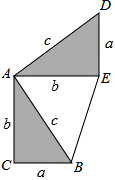 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程. 已知,DE∥AC,CD平分∠ACB,FE平分∠DEC,∠1与∠2互余,求证:DG∥EF.
已知,DE∥AC,CD平分∠ACB,FE平分∠DEC,∠1与∠2互余,求证:DG∥EF. 如图,数轴上的点A,B分别表示-3,2,则A,B两点间的距离是
如图,数轴上的点A,B分别表示-3,2,则A,B两点间的距离是
 如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件:
如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件: