题目内容
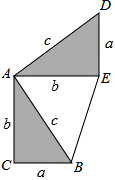 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.考点:勾股定理的证明
专题:
分析:首先连结BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,进而得出答案.
解答: 证明:连结BD,过点B作DE边上的高BF,则BF=b-a.
证明:连结BD,过点B作DE边上的高BF,则BF=b-a.
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=
ab+
b2+
ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=
ab+
c2+
a(b-a),
∴
ab+
b2+
ab=
ab+
c2+
a(b-a),
∴a2+b2=c2.
 证明:连结BD,过点B作DE边上的高BF,则BF=b-a.
证明:连结BD,过点B作DE边上的高BF,则BF=b-a.∵S五边形ACBED=S△ACB+S△ABE+S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2.
点评:此题主要考查了勾股定理得证明,表示出五边形面积是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、相等的角是对顶角 |
| B、一对同旁内角的平分线互相垂直 |
| C、对顶角的平分线在一条直线上 |
| D、同位角相等 |
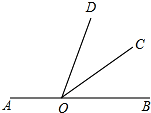 如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=36°,则∠AOD等于( )
如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=36°,则∠AOD等于( )| A、72° | B、100° |
| C、108° | D、144° |
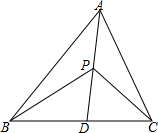 如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )
如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )| A、AB+PC>AC+PB |
| B、AB+PC<AC+PB |
| C、AB+PC=AC+PB |
| D、不确定 |
 如图为一张椅子的侧面视图,图中∠1和∠2是一对( )
如图为一张椅子的侧面视图,图中∠1和∠2是一对( )| A、同旁内角 | B、内错角 |
| C、同位角 | D、对顶角 |
若m是一个有理数,则
-m一定是( )
| 5 |
| A、正数 | B、负数 |
| C、有理数 | D、无理数 |
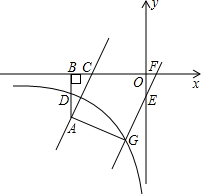 如图,点A在反比例函数y=
如图,点A在反比例函数y= 如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.
如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.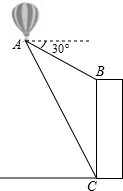 如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.
如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.