题目内容
等腰三角形一腰上的高与腰长之比为1:2,则等腰三角形顶角的度数为( )
| A、60° |
| B、120° |
| C、30°或150° |
| D、60°或120° |
考点:含30度角的直角三角形,等腰三角形的性质
专题:分类讨论
分析:当三角形为锐角三角形时,可求得其顶角为30°;当三角形为钝角三角形时,可求得顶角的邻补角为30°,可分别求得其顶角.
解答:解:当该三角形为锐角三角形时,如图1,

∵sin∠A=
=
,
∴∠A=30°,即△ABC的顶角为30°;
当该三角形为钝角三角形时,如图2,

在Rt△ABD中,∵sin∠BAD=
=
,
∴∠BAD=30°,
∴∠BAC=150°,即△ABC的顶角为150°;
综上可知该三角形的顶角为30°或150°,
故选C.

∵sin∠A=
| BD |
| AB |
| 1 |
| 2 |
∴∠A=30°,即△ABC的顶角为30°;
当该三角形为钝角三角形时,如图2,

在Rt△ABD中,∵sin∠BAD=
| BD |
| AB |
| 1 |
| 2 |
∴∠BAD=30°,
∴∠BAC=150°,即△ABC的顶角为150°;
综上可知该三角形的顶角为30°或150°,
故选C.
点评:本题主要考查含30°角的直角三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图为一张椅子的侧面视图,图中∠1和∠2是一对( )
如图为一张椅子的侧面视图,图中∠1和∠2是一对( )| A、同旁内角 | B、内错角 |
| C、同位角 | D、对顶角 |
若m是一个有理数,则
-m一定是( )
| 5 |
| A、正数 | B、负数 |
| C、有理数 | D、无理数 |
下列图形中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
若y=(m-2)xm2-m是关于x的二次函数,则常数m的值为( )
| A、-1 | B、2 |
| C、-2 | D、-1或-2 |
 如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.
如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为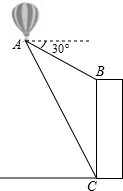 如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.
如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.