题目内容
 已知,DE∥AC,CD平分∠ACB,FE平分∠DEC,∠1与∠2互余,求证:DG∥EF.
已知,DE∥AC,CD平分∠ACB,FE平分∠DEC,∠1与∠2互余,求证:DG∥EF.考点:平行线的判定与性质
专题:证明题
分析:如图,由平行线的性质和角平分线的定义可先求得∠CHE=90°,又可得∠GDC=90°,可证明DG∥EF.
解答: 证明:如图,∵DE∥AC,
证明:如图,∵DE∥AC,
∴∠DEC+∠ECA=180°,
又∵CD平分∠ACB,FE平分∠DEC,
∴2∠DCE+2∠FEC=180°,
∴∠DCE+∠FEC=90°,
∴∠EGC=90°,
又∵∠1+∠2=90°,
∴∠GDC=90°,
∴∠GDC=∠CHE,
∴DG∥EF.
 证明:如图,∵DE∥AC,
证明:如图,∵DE∥AC,∴∠DEC+∠ECA=180°,
又∵CD平分∠ACB,FE平分∠DEC,
∴2∠DCE+2∠FEC=180°,
∴∠DCE+∠FEC=90°,
∴∠EGC=90°,
又∵∠1+∠2=90°,
∴∠GDC=90°,
∴∠GDC=∠CHE,
∴DG∥EF.
点评:本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
下列说法正确的是( )
| A、相等的角是对顶角 |
| B、一对同旁内角的平分线互相垂直 |
| C、对顶角的平分线在一条直线上 |
| D、同位角相等 |
若m是一个有理数,则
-m一定是( )
| 5 |
| A、正数 | B、负数 |
| C、有理数 | D、无理数 |
若y=(m-2)xm2-m是关于x的二次函数,则常数m的值为( )
| A、-1 | B、2 |
| C、-2 | D、-1或-2 |
若(ab3)3<0,则a与b的关系是( )
| A、异号 | B、同号 |
| C、都不为零 | D、关系不确定 |
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为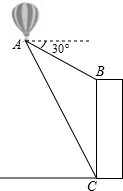 如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.
如图,热气球上的自动探测仪显示:从热气球的吊篮A观测一栋高楼的顶部B的俯角为30°,观测这栋高楼的底部C的俯角为60°,热气球的吊篮A此时的高度为180米,求这栋高楼的高度.