题目内容
 如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:AP是∠BAC的角平分线.
考点:角平分线的性质
专题:证明题
分析:根据HL定理得出Rt△AFP≌Rt△AEP,由此可得出结论.
解答:解:∵PE⊥AB,PF⊥AC,
∴∠AFP=∠AEP=90°.
在Rt△AFP与Rt△AEP中,
,
∴Rt△AFP≌Rt△AEP(HL),
∴PF=PE,
∴AP是∠BAC的角平分线.
∴∠AFP=∠AEP=90°.
在Rt△AFP与Rt△AEP中,
|
∴Rt△AFP≌Rt△AEP(HL),
∴PF=PE,
∴AP是∠BAC的角平分线.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将抛物线y=x2向下平移2个单位,再向左平移1个单位,则得到的抛物线解析式是( )
| A、y=(x-1)2-2 |
| B、y=(x+1)2+2 |
| C、y=(x-1)2+2 |
| D、y=(x+1)2-2 |
 如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=
如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA= 如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是
如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是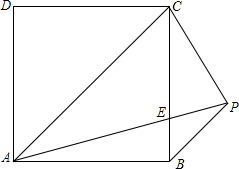 如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP.
如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP.