题目内容
 如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=
如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=| 3 |
考点:切线的性质,扇形面积的计算
专题:压轴题
分析:连接OA,PA切⊙O于A,则∠A=90°,设⊙O的半径为x,则在Rt△OAP中,根据勾股定理列方程求出⊙O的半径,再根据三角形函数确定∠P,∠AOB的度数,利用阴影部分的面积=S△PAO-S扇形OAB,代入数值即可求值.
解答: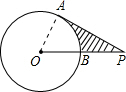 解:连接OA,∵PA切⊙O于A,
解:连接OA,∵PA切⊙O于A,
∴∠A=90°,设⊙O的半径为x,
∴在Rt△OAP中,
PO2=OA2+PA2,
即(1+x)2=x2+(
)2,
解得x=1,tanP=OA:PA=1:
,
∴∠P=30°,∠AOB=60°,
∴阴影部分的面积=S△PAO-S扇形OAB=
×1×
=
-
=
.
 解:连接OA,∵PA切⊙O于A,
解:连接OA,∵PA切⊙O于A,∴∠A=90°,设⊙O的半径为x,
∴在Rt△OAP中,
PO2=OA2+PA2,
即(1+x)2=x2+(
| 3 |
解得x=1,tanP=OA:PA=1:
| 3 |
∴∠P=30°,∠AOB=60°,
∴阴影部分的面积=S△PAO-S扇形OAB=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| π |
| 6 |
3
| ||
| 6 |
点评:本题考查切线的性质、勾股定理、直角三角形、扇形的面积公式、三角形函数,解决问题得关键是利用勾股定理列方程求出圆的半径.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
已知命题“关于x的方程bx+1=0必有解”,能说明这个命题是假命题的一个反例是( )
| A、b=-1 | B、b=2 |
| C、b=-2 | D、b=0 |
在△ABC中,锐角A、B满足|sinA-
|+[cos(B-15°)-
]2=0,则△ABC是( )
| ||
| 2 |
| ||
| 2 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
 如图,已知BC是⊙O的直径,过点B的弦BD平行于半径OA,若∠B的度数是50°,则∠C的度数是( )
如图,已知BC是⊙O的直径,过点B的弦BD平行于半径OA,若∠B的度数是50°,则∠C的度数是( )| A、50° | B、40° |
| C、30° | D、25° |
 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题: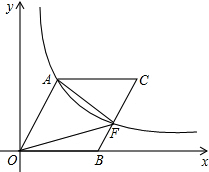 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB= 如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.