题目内容
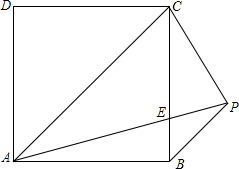 如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP.
如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP.考点:含30度角的直角三角形,等腰三角形的性质,正方形的性质
专题:证明题
分析:把△ABP顺时针旋转90°得到△ADG,从而可得B、G、D三点在同一条直线上,然后可以证明△AGD与△CGD全等,根据全等三角形对应边相等可得AG=CG,所以△AGC为等边三角形,根据等边三角形的性质可以推出∠CEP=∠CPE=75°,从而得解.
解答:证明:∵四边形ABCD是正方形,
∴AC⊥AB,AD=AB=CD,∠ACB=45°,
∵BP∥AC,
∴∠CBP=∠CB=45°,∠ABP=90°+45°=135°,
把△ABP绕A旋转90°到△ADG,连接CG,如图,
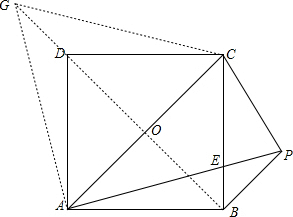
则△ABP≌△ADG,
∵四边形ABCD是正方形,
∴∠BDA=∠CDB=45°,
所以AG=AP,∠ADG=∠ABP=135°,∠PAB=∠DAG,
则B、D、G三点共线,
∴∠CDG=∠ADG=135°,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴AG=CG=AP=AC,
∴△AGC是等边三角形,
∵AC⊥BD,
∴∠CGD=∠AGD=30°,
∴∠GAD=∠BAP=60°-45°=15°,
∴∠CAP=45°-15°=30°,
∵AC=AP,
∴∠ACP=∠APC=75°,
∴∠ECP=75°-45°=30°,
∴∠CEP=180°-30°-75°=75°,
∴∠CPE=∠CEP,
∴CE=CP.
∴AC⊥AB,AD=AB=CD,∠ACB=45°,
∵BP∥AC,
∴∠CBP=∠CB=45°,∠ABP=90°+45°=135°,
把△ABP绕A旋转90°到△ADG,连接CG,如图,

则△ABP≌△ADG,
∵四边形ABCD是正方形,
∴∠BDA=∠CDB=45°,
所以AG=AP,∠ADG=∠ABP=135°,∠PAB=∠DAG,
则B、D、G三点共线,
∴∠CDG=∠ADG=135°,
在△ADG和△CDG中,
|
∴△ADG≌△CDG(SAS),
∴AG=CG=AP=AC,
∴△AGC是等边三角形,
∵AC⊥BD,
∴∠CGD=∠AGD=30°,
∴∠GAD=∠BAP=60°-45°=15°,
∴∠CAP=45°-15°=30°,
∵AC=AP,
∴∠ACP=∠APC=75°,
∴∠ECP=75°-45°=30°,
∴∠CEP=180°-30°-75°=75°,
∴∠CPE=∠CEP,
∴CE=CP.
点评:本题考查了全等三角形的性质和判定,正方形的性质,旋转的性质的应用,根据旋转得出全等图形是解此题的关键.

练习册系列答案
相关题目
下列各式不是同类项的是( )
| A、a2b与3a2b | ||
| B、x与2x | ||
C、
| ||
D、
|
 如图,已知BC是⊙O的直径,过点B的弦BD平行于半径OA,若∠B的度数是50°,则∠C的度数是( )
如图,已知BC是⊙O的直径,过点B的弦BD平行于半径OA,若∠B的度数是50°,则∠C的度数是( )| A、50° | B、40° |
| C、30° | D、25° |
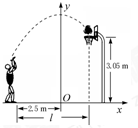 小敏在某次投篮中,球的运动线路是抛物线y=-
小敏在某次投篮中,球的运动线路是抛物线y=-| 1 |
| 5 |
| A、3.5m | B、4m |
| C、4.5m | D、4.6m |

 如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.